بروریختی
در نظریه رستهها، یک بروریختی یک پیکان f: X → Y است که قانون حذف از سمت راست بر آن صادق است، به این معنا که برای هر دو ریخت g۱, g۲: Y → Z, .
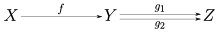
بروریختیها، مشابه رسته توابع پوشا هستند (و در رسته مجموعهها، این مفهوم منطبق بر توابع پوشاست) اما ممکن است که این دقیقاً در همه جا برقرار نباشد؛ به عنوان مثال، تابع شمول یک بروریختی حلقه ایست. دوگان یک بروریختی، یک تکریختی است. (یعنی یک بروریختی در یک رسته ی C، یک تکریختی در رسته دوگان Cop است).
بسیاری از مؤلفان در جبر مجرد و جبر جهانی، یک بروریختی را به سادگی بعنوان یک همریختی بِرویِ یا پوشا تعریف میکنند. هر بروریختی در این نگاه جبری، یک بروریختی در منظر نظریه رسته هاست، اما عکس این مسئله در همهٔ رستهها برقرار نیست. در این مقاله اصطلاح «بروریختی»، در چارچوب نظریه رستههای فوق استفاده خواهد شد. برای مطالعه بیشتر در این باره، مراجعه کنید به بخش اصطلاحات در پایین.
مثال ویرایش
هر ریخت در یک رسته سفت که تابع زیربنایی اش پوشاست، یک بروریختی است. در بسیاری از رستههای سفت مورد توجه، عکس این قضیه نیز درست است. برای مثال در رستههای زیر، بروریختیها دقیقاً همان ریختهایی اند که روی مجموعههای زیربنایی، پوشا هستند:
- Set، از مجموعهها و توابع. برای اثبات اینکه هر بروریختی f: X → Y در Set پوشاست، آن را هم با تابع مشخصه g۱: Y → {۰٬۱} از تصویر f(X) و هم نگاشت g۲: Y → {۰٬۱} که برابر ثابت ۱ است، ترکیب میکنیم.
- Rel، از مجموعهها با روابط دوتایی و توابع حافظ رابطه. در اینجا میتوانیم همان اثباتِ Set را مورد استفاده قرار دهیم، در صورت تجهیز {۰٬۱} با رابطه {۰٬۱}×{0,1}.
- Grp، از گروهها و همریختیهای گروهی. این نتیجه که هر بروریختی در Grp پوشاست، دستاورد اتو شرایر است (او در واقع بیش از این را ثابت کرد؛ اینکه هر زیرگروه یک تساوی ساز است، با استفاده از ضرب آزادبا یک زیرگروه ادغام شده)؛ اثباتی مقدماتی را میتوان در (Linderholm 1970) یافت.
جستارهای وابسته ویرایش
منابع ویرایش
- Adámek, Jiří, Herrlich, Horst, & Strecker, George E. (1990). Abstract and Concrete Categories بایگانیشده در ۲۱ آوریل ۲۰۱۵ توسط Wayback Machine (4.2MB PDF). Originally publ. John Wiley & Sons. ISBN 0-471-60922-6. (now free on-line edition)
- Bergman, George M. (1998), An Invitation to General Algebra and Universal Constructions, Harry Helson Publisher, Berkeley. ISBN 0-9655211-4-1.
- "Epimorphism", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Linderholm, Carl (1970). A Group Epimorphism is Surjective. American Mathematical Monthly 77, pp. 176–177. Proof summarized by Arturo Magidin in [۱].
- Lawvere & Rosebrugh: Sets for Mathematics, Cambridge university press, 2003. ISBN 0-521-80444-2.

