نمره استاندارد

در آمار، نمره استاندارد مضربی از انحراف معیار است که مقدار آن، نشان می‌دهد یک نمره خام (یعنی مقدار مشاهده شده یا یک نقطه از داده) چقدر بالاتر یا کمتر از میانگین مقدار مشاهده یا اندازه‌گیری شده‌است. نمرات خام بالاتر از میانگین دارای نمره استاندارد مثبت و نمرات زیر میانگین دارای نمره استاندارد منفی هستند.^[۱]^[۲]^[۳]^[۴]

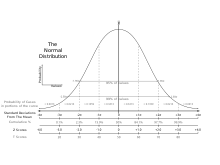
نمره استاندارد، با کسر میانگین جمعیت از یک نمره خام فردی و سپس تقسیم آن بر انحراف معیار جمعیت محاسبه می‌شود. این فرایند تبدیل نمره خام به یک نمره استاندارد، نرمال سازی نامیده می‌شود (اگرچه نمره استاندارد تنها راه نرمال سازی نیست).^[۵]

نمرات استاندارد را معمولاً z-score می‌ نامند. این دو لفظ ممکن است به جای یک‌دیگر استفاده شوند. اصطلاحات دیگر شامل z-values، نمرات نرمال و متغیرهای استاندارد می‌باشد.^[۶]

در کنکور سراسری، مبنای محاسبه رتبه داوطلبان، این نمره است.^[۷]

محاسبه

اگر میانگین جمعیت و انحراف معیار جمعیت مشخص باشد، نمره خام x به این صورت به یک تراز تبدیل می‌شود.

z={x-\mu  \over \sigma }

به صورتی که:

μ برابر میانگین جمعیت است.

σ برابر انحراف معیار جمعیت است.

مقدار مطلق z فاصله بین آن نمره خامِ x و میانگین جمعیت را در همان یکای انحراف معیار نشان می‌دهد. وقتی نمره خام زیر میانگین باشد، z منفی است و وقتی بالاتر باشد، مثبت است.

مقدار تراز (نمره ای که در کنکور سراسری از آن استفاده می‌شود)، برای هر درس به نحوه زیر محاسبه می‌گردد:

$T=1000Z+5000$

به صورتی که Z برابر نمره استاندارد است.

پانویس

↑ Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (Fourth ed.), McGraw Hill, ISBN 978-0-07-148584-5
↑ Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (Fifth ed.), Pearson / Prentice Hall, ISBN 978-0131877061
↑ Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (Third ed.), McGraw Hill, ISBN 978-0071824118
↑ Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (First ed.), Chapman & Hall / CRC Press, ISBN 978-1439873380
↑ Mulders, Martijn; Zanderighi, Giulia, eds. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.
↑ Gross, Eilam (2017-11-06). "Practical Statistics for High Energy Physics". CERN Yellow Reports: School Proceedings (به انگلیسی). 4/2017: 165–186. doi:10.23730/CYRSP-2017-004.165.
↑ Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (Fourth ed.), McGraw Hill, ISBN 978-0073014661

[SpiegelStephens2008-1] Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (Fourth ed.), McGraw Hill, ISBN 978-0-07-148584-5

[Mendenhall2007-2] Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (Fifth ed.), Pearson / Prentice Hall, ISBN 978-0131877061

[GlantzSlinker2016-3] Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (Third ed.), McGraw Hill, ISBN 978-0071824118

[Aho2014-4] Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (First ed.), Chapman & Hall / CRC Press, ISBN 978-1439873380

[5] Mulders, Martijn; Zanderighi, Giulia, eds. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.

[6] Gross, Eilam (2017-11-06). "Practical Statistics for High Energy Physics". CERN Yellow Reports: School Proceedings (به انگلیسی). 4/2017: 165–186. doi:10.23730/CYRSP-2017-004.165.

[KutnerNachtsheim2004-7] Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (Fourth ed.), McGraw Hill, ISBN 978-0073014661

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]