متوازی‌السطوح

متوازی‌السطوح
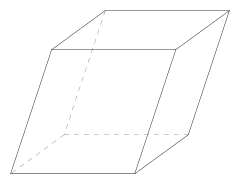
نوع حجم	منشور
وجه‌ها	۶ متوازی‌الاضلاع
رأس‌ها	۱۲
یال‌ها	۸
گروه تقارن	Ci, [۲+,۲+], (1×)
خاصیت	convex

در هندسه، متوازی‌السطوح یک حجم هندسی است که از شش وجه تشکیل شده و هر یک از این وجه‌ها متوازی‌الاضلاع بوده و هر دو وجه مقابل متساوی و متوازی است. متوازی‌السطوح از انواع منشور است.

متوازی‌السطوح با بردارها در فضای سه‌بعدی

رابطه

چهار وجهی مربوطه

حجم هر چهار وجهی که دارای سه یال همگرای متوازی الاضلاع است، حجمی برابر با یک ششم حجم آن متوازی الاضلاع دارد.

رابطه متوازی السطوح با مکعب

حجم یک متوازی السطوح با ضلع های مساوی با مکعب باهم برابر اند.

خواص

• هر یک از سه جفت وجه موازی را می توان به عنوان صفحات پایه منشور مشاهده کرد. یک متوازی الاضلاع دارای سه مجموعه از چهار یال موازی است. لبه های هر مجموعه دارای طول مساوی هستند.

• متوازی الاضلاع از تبدیل های خطی یک مکعب (برای موارد غیر انحطاط: تبدیل خطی دوطرفه) حاصل می شود.

• از آنجایی که هر وجه دارای تقارن نقطه ای است , متوازی الاضلاع یک زونهدرون است . همچنین کل متوازی الاضلاع دارای تقارن نقطه ای C _i است (همچنین به triclinic مراجعه کنید ). هر صورت، از بیرون، تصویر آینه ای از چهره مقابل است. صورت ها به طور کلی کایرال هستند ، اما موازی شکل نیست.

• با رونوشت‌های همخوان از هر موازی‌پایه‌ای امکان‌پذیر است که فضا را پر کند.

• اگر همه ضلع های مکعب را به یک زاویه برابر مورب کنیم به یک متوازی السطوح تبدیل می شود که تمام وجه هایش لوزی است و مساحت وجه های متوازی السطوح با با مساحت وجه های مکعب برابر است.
• متوازی السطوح از انواع منشورها است
• متوازی السطوح را می توان یکی از چندوجهی ها گفت

حجم

متوازی السطوح حجمی است که از سه بردار سه بعدی a,b,cدرست شده است و با ضرب خارجی بردار ها درست شده است.

اضلاع متوازی السطوح بر اساسa,b,c

محاسبه حجم

ابتدا متوازی السطوحی رسم می کنیم که در فضای برداری باشد و در فضای سه بعدیR³قرار می دهیم.بردار های آن اینگونه است که:

1. $S=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|$
2. $h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|$

محاسبه حجم اینگونه است مساحت قاعده بر اساس مساحت متوازی الاضلاع بدست آید و ارتفاع آن بر اساس رابطه فیثاغورس بدست آید.پس حجم متوازی السطوح برابر با این رابطه است.

$$V=B\cdot h=\left(\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \gamma \right)\cdot \left|\mathbf {c} \right|\left|\cos \theta \right|=\left|\mathbf {a} \times \mathbf {b} \right|\left|\mathbf {c} \right|\left|\cos \theta \right|=\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|.$$

کسینوس تتا و سینوس تتا در محاسبه قدر مطلق برابر با یک می شود،قدرمطلق مساحت برداری هایa,b,cبرابر با خودشان است.

می توان به روش عمیق تری حجم آن را بدست آورد،ضرب داخلی بردار های خارجی که با ضرب خارجی این سه بردار متوازی السطوح را بدست آورند این گونه است.$\mathbf {a} =(a_{1},a_{2},a_{3})^{\mathsf {T}},~\mathbf {b} =(b_{1},b_{2},b_{3})^{\mathsf {T}},~\mathbf {c} =(c_{1},c_{2},c_{3})^{\mathsf {T}},$حجم برابر است

$V=\left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.$

که همان برابر با این رابطه است.

$$V=\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|.={\displaystyle \left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.}$$

راه دیگر برای اثبات ( V1 ) استفاده از مولفه اسکالر در جهت استa×b

از بردار:a,b,c

$${\begin{aligned}V=\left|\mathbf {a} \times \mathbf {b} \right|\left|\operatorname {scal} _{\mathbf {a} \times \mathbf {b} }\mathbf {c} \right|=\left|\mathbf {a} \times \mathbf {b} \right|{\frac {\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|}{\left|\mathbf {a} \times \mathbf {b} \right|}}=\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|.\end{aligned}}$$

نتیجه بر این است.

حجم متوازی السطوح به صورت مختصاتی برابر با این رابطه است:$V=|({\vec {a}}.{\vec {b}}).{\vec {c}}|=a_{1}b_{1}c_{1}+a_{2}b_{2}c_{2}+a_{3}b_{3}c_{3}$

حجم متوازی السطوح به صورت مختصاتی برابر با این عبارت فوق است اما به روش دیگر هم که به صورت مختصاتی نوشته نمی گردد بلکه مثل حجم مکعب مستطیل است که برابر با ضرب طول بردار هاست ولی یک عبارتی لازم دارد. نتیجه بر این است که عبارت مجهول:

با استفاده از روش قدر مطلق و محاسبه ضرب داخلی و خارجی بردارها به مقداری به نامkنیاز است.kمقداری است که بر اساس زاویه های لبه متوازی السطوح بدست می آید.که به صورت جذر آن درحجم متوازی السطوح به کار می رود.

مقدار kبراساس این رابطه بدست می آید.

$$K={1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )},$$

مقدار جذر آن این گونه است

$${\sqrt {K}}={\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}},$$

حجم آن براساس این رابطه نوشته می گردد.

$$V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}},$$

که می توان این گونه نوشت

$$V=abc{\sqrt {K}}$$

مساحت

مساحت یک متوازی السطوح براساس جمع مساحت شش متوازی الاضلاع بدست می آید که براساس این رابطه نوشته می گردد

$${\begin{aligned}A&=2\cdot \left(|\mathbf {a} \times \mathbf {b} |+|\mathbf {a} \times \mathbf {c} |+|\mathbf {b} \times \mathbf {c} |\right)\\&=2\left(ab\sin \gamma +bc\sin \alpha +ca\sin \beta \right).\end{aligned}}$$

مساحت متوازی السطوح مثل مساحت مکعب مستطیل بدست می آید،مکعب،مکعب مستطیل از احجام منشوری است که به صورت برداری کشیده اند.

به صورت دیگر هم مساحت آن پیدا می گردد که به صورت مساحت متوازی الاضلاع بدست می آید

برای پیدا کردن مساحت متوازی السطوج بر اساس a,b,c اینگونه است.

$2{(ah+bh'+ch'')}$

hبرابر با ارتفاع متوازی السطوح است بر حسب تتا زاویه است که h بر اساس رابطه فیثاغورس نوشته میشود.

${h^{2}=a^{2}-x^{2}}$

${h'^{2}=a^{2}-y^{2}}$

${h''^{2}=a^{2}-z^{2}}$

$x,y,z$=مقداری است که بر اساس تتا زیر جزئی از طول های به ترتیب b,c است

اگر این دو رابطه را محاسبه کنیم به این نتیجه می رسیم

$${\begin{aligned}A&=2\cdot \left(|\mathbf {a} \times \mathbf {b} |+|\mathbf {a} \times \mathbf {c} |+|\mathbf {b} \times \mathbf {c} |\right)\\&=2\left(ab\sin \gamma +bc\sin \alpha +ca\sin \beta \right).\end{aligned}}={\displaystyle 2{(ah+bh'+ch'')}}$$

منابع

Wikipedia contributors, "Parallelepiped," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Parallelepiped&oldid=539519980 (accessed April 12, 2013).