پلیلگاریتم
تابع پلیلگاریتم با جمع سری توانی زیر مشخص میشود:
این تعریف برای آرگومانهای مختلط z به شرط اندازه z بزرگتر از ۱ معتبر است.
دلیل انتخاب این اسم این است که این تابع از انتگرال خودش به دست میآید:
بنابراین دی لگاریتم انتگرال لگاریتم است و به همین ترتیب. برای sهای غیرمنفی حقیقی تابع پلی لگاریتم یک تابع گویا است.
 |
 |
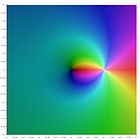 |
 |
 |
 |
 |
| Li−3(z) | Li−2(z) | Li−1(z) | Li0(z) | Li1(z) | Li2(z) | Li3(z) |
منابع
ویرایش- Abramowitz, M. ; Stegun, I.A. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications. ISBN 0-486-61272-4.
- Apostol, T.M. (2010), "Polylogarithm", in Olver, Frank W. J. ; Lozier, Daniel M. ; Boisvert, Ronald F. ; Clark, Charles W. , NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255، MR 2723248

