منحنی ویژگی عملیاتی گیرنده

منحنی ویژگی عملیاتی گیرنده یا منحنی مشخصه عملکرد سامانه (به انگلیسی: Receiver operating characteristic) یک روش کمی ارزیابی در مسائل طبقه‌بندی است که با ROC نشان داده می‌شود.

این روش در فیزیک پزشکی برای مقایسه اختلاف روش‌های تصویربرداری به کار می‌رود. در این روش، هدف این است که توانایی آسیب‌شناسی یک سامانه دقیقاً ارزیابی شود، لذا از معیارهایی که بر اساس قضاوت و تصمیم اشخاص است استفاده می‌شود.

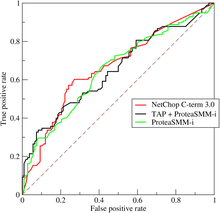
منحنی ROC با رسم نرخ مثبت واقعی (TPR) در برابر نرخ مثبت کاذب (FPR) در تنظیم آستانه‌های مختلف ایجاد می‌شود. نرخ مثبت واقعی به‌عنوان حساسیت، بازیابی یا احتمال تشخیص نیز شناخته می‌شود. نرخ مثبت کاذب نیز به عنوان احتمال هشدار کاذب شناخته می‌شود و می‌تواند به عنوان (ویژگی - ۱) محاسبه شود. ROC همچنین می‌تواند به عنوان نموداری از توان آماری به عنوان تابعی از خطای نوع اول قاعده تصمیم در نظر گرفته شود (زمانی که عملکرد فقط از نمونه‌ای از جامعه محاسبه می‌شود، می‌توان آن را به عنوان تخمینگر این کمیت‌ها در نظر گرفت). بنابراین منحنی ROC حساسیت یا بازیابی به عنوان تابعی از نرخ مثبت کاذب است. به‌طور کلی، اگر توزیع احتمال برای هر دو تشخیص و هشدار نادرست شناخته شده باشد، منحنی ROC را می‌توان با رسم تابع توزیع تجمعی (ناحیه زیر توزیع احتمال از$-\infty$ تا آستانه تشخیص) احتمال تشخیص در محور y در مقابل تابع توزیع تجمعی احتمال هشدار کاذب در محور x ایجاد کرد.

ROC همچنین به عنوان یک منحنی ویژگی عملکرد نسبی شناخته می‌شود، زیرا مقایسه دو ویژگی عملیاتی (TPR و FPR) به عنوان تغییر معیار است.

مفاهیم اولیه

یک مدل طبقه‌بندی یک نگاشت از نمونه‌های بین کلاس‌ها/گروه‌های خاص است. از آنجایی که طبقه‌بندی‌کننده یا نتیجه تشخیص می‌تواند یک عدد حقیقی دلخواه باشد (خروجی پیوسته)، مرز طبقه‌بندی‌کننده بین کلاس‌ها باید با یک مقدار آستانه تعیین شود (به عنوان مثال، برای تعیین اینکه آیا یک فرد بر اساس اندازه‌گیری فشار خون مبتلا به فشار خون بالا است یا خیر). یا می‌تواند یک برچسب کلاس گسسته باشد که یکی از کلاس‌ها را نشان می‌دهد.

یک مشکل پیش‌بینی دو طبقه‌ای (طبقه‌بندی دودویی) را در نظر بگیرید که در آن نتایج به صورت مثبت (p) یا منفی (n) برچسب‌گذاری می‌شوند. چهار نتیجه ممکن از یک طبقه‌بندی کننده باینری وجود دارد. اگر نتیجه یک پیش‌بینی p باشد و مقدار واقعی نیز p باشد، آن را مثبت واقعی (TP) می‌گویند. با این حال اگر مقدار واقعی n باشد، گفته می‌شود که مثبت کاذب (FP) است. برعکس، منفی واقعی (TN) زمانی رخ می‌دهد که هم نتیجه پیش‌بینی و هم مقدار واقعی n باشد، و منفی کاذب (FN) زمانی رخ می‌دهد که نتیجه پیش‌بینی n باشد در حالی که مقدار واقعی p باشد. برای به دست آوردن مثال مناسب در یک مشکل دنیای واقعی، یک آزمایش تشخیصی را در نظر بگیرید که به دنبال تعیین اینکه آیا یک فرد به بیماری خاصی مبتلا است یا خیر. مثبت کاذب در این مورد زمانی اتفاق می‌افتد که آزمایش فرد مثبت باشد، اما در واقع به بیماری مبتلا نباشد. از سوی دیگر، منفی کاذب زمانی اتفاق می‌افتد که آزمایش فرد منفی باشد و نشان دهد که او سالم است، در حالی که واقعاً به این بیماری مبتلا است.

فضای مشخصه عملکرد سیستم

فضای ROC برای یک طبقه‌بند بهتر و بدتر

جدول پیشایندی می‌تواند چندین «متریک» ارزیابی را استخراج کند. برای رسم منحنی ROC، فقط نرخ مثبت واقعی (TPR) و نرخ مثبت کاذب (FPR) مورد نیاز است (به عنوان توابع برخی از پارامترهای طبقه‌بندی کننده). TPR تعیین می‌کند که چه تعداد از نتایج مثبت صحیح در بین تمام نمونه‌های مثبت موجود در طول آزمایش رخ می‌دهد. از سوی دیگر، FPR تعیین می‌کند که چه تعداد از نتایج مثبت نادرست در بین تمام نمونه‌های منفی موجود در طول آزمایش رخ می‌دهد. فضای ROC توسط FPR و TPR به ترتیب به عنوان محورهای x و y تعریف می‌شود که مبادلات نسبی بین مثبت واقعی (منافع) و مثبت کاذب (هزینه‌ها) را نشان می‌دهد. از آنجایی که TPR معادل حساسیت و FPR برابر با (ویژگی - ۱) است، نمودار ROC گاهی اوقات نمودار حساسیت در مقابل (ویژگی - ۱) نامیده می‌شود. هر نتیجه پیش‌بینی یا نمونه‌ای از یک ماتریس درهم‌ریختگی نشان‌دهنده یک نقطه در فضای ROC است.

بهترین روش پیش‌بینی ممکن نقطه‌ای را در گوشه بالا سمت چپ یا مختصات (۰٬۱) فضای ROC به دست می‌دهد که نشان‌دهنده ۱۰۰٪ حساسیت (بدون منفی کاذب) و ۱۰۰٪ ویژگی (بدون مثبت کاذب) است. نقطه (۰٬۱) طبقه‌بندی کامل نیز نامیده می‌شود. یک حدس تصادفی یک نقطه در امتداد یک خط مورب (به اصطلاح خط بدون تبعیض) از پایین سمت چپ به گوشه سمت راست بالا (بدون در نظر گرفتن نرخ پایه مثبت و منفی) نشان می‌دهد. یک مثال شهودی از حدس زدن تصادفی، تصمیم‌گیری با چرخاندن سکه است. با افزایش اندازه نمونه، نقطه ROC طبقه‌بندی‌کننده تصادفی به سمت خط مورب متمایل می‌شود. در مورد سکه متعادل، به نقطه (۰٫۵، ۰٫۵) تمایل دارد. قطر فضای ROC را تقسیم می‌کند. نقاط بالای مورب نتایج طبقه‌بندی خوبی را نشان می‌دهد (بهتر از تصادفی). نقاط زیر خط نشان دهنده نتایج بد (بدتر از تصادفی) است. توجه داشته باشید که خروجی یک پیش‌بینی‌کننده دائماً بد می‌تواند به سادگی معکوس شود تا یک پیش‌بین خوب به دست آید.

منحنی‌ها در فضای مشخصه عملکرد سیستم

در طبقه‌بندی باینری، پیش‌بینی کلاس برای هر نمونه اغلب بر اساس یک متغیر تصادفی پیوسته $X$ انجام می‌شود که یک «امتیاز» محاسبه‌شده برای نمونه است (مثلاً احتمال تخمین زده‌شده در رگرسیون لجستیک). با توجه به پارامتر آستانه $T$، نمونه به عنوان «مثبت» در صورت $X>T$ و در غیر این صورت «منفی» طبقه‌بندی می‌شود. $X$ چگالی احتمال $f_{1}(x)$ را دنبال می‌کند اگر نمونه واقعاً به کلاس «مثبت» تعلق دارد و $f_{0}(x)$ اگر غیر از این باشد؛ بنابراین، نرخ مثبت واقعی توسط ${\mbox{TPR}}(T)=\int _{T}^{\infty }f_{1}(x)\,dx$ و نرخ مثبت کاذب توسط ${\mbox{FPR}}(T)=\int _{T}^{\infty }f_{0}(x)\,dx$ مشخص می‌شود. منحنی عملیاتی گیرنده به صورت پارامتری ${\mbox{TPR}}(T)$ در مقابل ${\mbox{FPR}}(T)$ با $T$ به عنوان پارامتر متغیر ترسیم می‌کند.

به عنوان مثال، تصور کنید که سطح پروتئین خون در افراد بیمار و افراد سالم به ترتیب با میانگین‌های ۲ گرم در دسی لیتر و ۱ گرم در دسی لیتر به صورت نرمال توزیع می‌شود. یک آزمایش پزشکی ممکن است سطح پروتئین خاصی را در نمونه خون اندازه‌گیری کند و هر عددی را بالاتر از یک آستانه مشخص به عنوان نشانه بیماری طبقه‌بندی کند. آزمایشگر می‌تواند آستانه را تنظیم کند (خط عمودی سبز در شکل)، که به نوبه خود نرخ مثبت کاذب را تغییر می‌دهد. افزایش آستانه منجر به مثبت کاذب کمتر (و منفی کاذب بیشتر) می‌شود که مربوط به حرکت به سمت چپ در منحنی است. شکل واقعی منحنی بر اساس میزان همپوشانی دو توزیع تعیین می‌شود.

جستارهای وابسته

• امتیاز اف ۱
• دقت و بازیابی
• نظریه تصمیم
• ماتریس درهم‌ریختگی