توزیع گاوسی معکوس تعمیمیافته
توزیع گاوسی معکوس تعمیمیافته (GIG : Generalized Inverse Gaussian) در نظریه احتمال و آمار یک توزیع پیوسته با سه پارامتر است. تابع چگالی احتمال این توزیع به صورت زیر است:
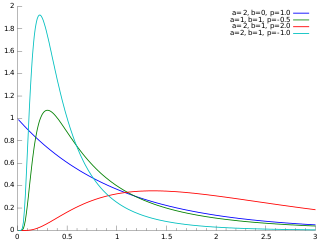 | |||
| پارامترها | |||
|---|---|---|---|
| تکیهگاه | |||
| Unknown type | |||
| میانگین | |||
| مُد | |||
| Unknown type | |||
| تابع مولد گشتاور | |||
مشخصات
ویرایشمجموع
ویرایشبارندورف-نیلسن (O. Barndorff-Nielsen) و هالگرین (C. Halgreen) اثبات کردند که توزیع GIG بینهایت تقسیمپذیر است.[۱]
آنتروپی
ویرایشآنتروپی توزیع GIG به صورت زیر داده میشود:
توزیعهای مرتبط
ویرایشتوزیع گاوسی معکوس و توزیع گاما حالتهای خاصی از توزیع گاوسی معکوس تعمیمیافته با و هستند.[۲]
به طور دقیق، یک توزیع گاوسی معکوس با فرم
یک توزیع گاوسی معکوس تعمیمیافته با ، و است.
یک توزیع گاما با فرم
یک توزیع گاوسی معکوس تعمیمیافته با ، و است.
یک توزیع گاما معکوس، یک توزیع گاوسی معکوس تعمیمیافته با و است.[۳]
یک توزیع هایپربولیک، یک توزیع گاوسی معکوس تعمیمیافته با است.[۲]
کاربردهای احتمالی
ویرایش1) توزیع GIG به عنوان قانونی برای کسرهای مسلسل
ویرایشو را دو متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که و برای . در این صورت داریم اگر و فقط اگر .
، و را سه متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که ، و برای . در این صورت داریم اگر و فقط اگر .
به طور کلی اگر یک دنباله از متغیر تصادفیهای مستقل از هم باشد به طوری که و برای ، آنگاه داریم:
.[۴]
2) خاصیت Matsumoto-Yor
ویرایشدو متغیر تصادفی مثبت و مستقل از هم و را در نظر بگیرید به طوری که و برای . خاصیت Matsumoto-Yor بیان میکند که متغیر تصادفیهای و از هم مستقل هستند.[۵]
مثالهایی از کاربرد توزیع گاوسی معکوس تعمیمیافته
ویرایش- Jorgensen در سال 1982 ثابت کرد که توزیع GIG فیت مناسبتری نسبت به توزیع نمایی در داده های مورد استفاده در موارد زیر است:[۴]
- فواصل زمانی بین خرابیهای پیدرپی تجهیزات تهویهی هوا در هواپیمای بوئینگ 720
- فواصل زمانی بین ضربانها در یک فیبر عصبی
- فواصل زمانی بین رد شدن وسایل نقلیه از یک نقطه
- Iyengar و Liao در سال 1997: فعالیت عصبی؛ مقایسه بین فیت توزیع GIG و فیت توزیع نرمال لگاریتمی.[۴]
- Chebana et al در سال 2010: کاربرد در وقایع مفرط هیدرولوژیکی[۴]
منابع
ویرایش- ↑ O. Barndorff-Nielsen, Christian Halgreen (دسامبر ۱۹۷۷). «Infinite divisibility of the hyperbolic and generalized inverse Gaussian distributions» (PDF).
- ↑ ۲٫۰ ۲٫۱ Lloyd.، Johnson, Norman (©1994-©1995). Continuous univariate distributions (ویراست ۲nd ed). New York: Wiley. OCLC 29428092. شابک ۰۴۷۱۵۸۴۹۵۹. تاریخ وارد شده در
|تاریخ=را بررسی کنید (کمک) - ↑ Iverson, Cheryl (2009-04-01). "Package Inserts". AMA Manual of Style. doi:10.1093/jama/9780195176339.022.82.
- ↑ ۴٫۰ ۴٫۱ ۴٫۲ ۴٫۳ A. E. Koudou (مارس ۸, ۲۰۱۸). «The generalized inverse Gaussian distribution» (PDF). بایگانیشده از اصلی (PDF) در ۲۹ ژانویه ۲۰۱۹. دریافتشده در ۳۰ نوامبر ۲۰۱۸.
- ↑ Matsumoto, H. and Yor, M. (۲۰۰۱). «An analogue of Pitman's 2M - X theorem for exponential Wiener functional, Part II: the role of the generalized inverse Gaussian laws». Nagoya Math. J.
- Gérard Letac and Vanamamalai Seshadri، A characterization of the generalized inverse Gaussian distribution by continued fractions، Probability Theory and Related Fields, Vol 62 (1983)، pp. 485-489 doi:10.1007/BF00534200





![{\displaystyle {\Bigl (}{\frac {b}{a}}{\Bigl )}\left[{\frac {K_{p+2}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}-{\Biggl (}{\frac {K_{p+1}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}{\Biggr )}^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/388ab7e9eb161fc701ca9619687fa32a89128244)


