نگاره فاز
نگاره فاز یا فیز پرتره نمایش هندسی مسیرهای یک سامانه پویا در صفحه فاز است. هر مجموعه از شرایط اولیه با یک منحنی یا نقطه متفاوت نشان داده میشود.

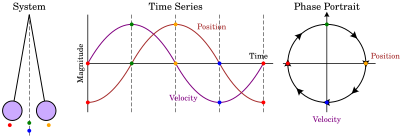
نگارههای فاز ابزاری ارزشمند در مطالعه سامانههای پویا هستند. آنها از یک رسم از سیرهای معمول در فضای حالت تشکیل شدهاند. این اطلاعاتی از قبیل وجود جاذب، دافع یا چرخه حدی برای مقدار پارامتر انتخاب شده را نشان میدهد. مفهوم همارزی توپولوژیک در طبقهبندی رفتار سیستمها با تعیین زمانی که دو نگاره فاز مختلف رفتار پویای کیفی یکسانی را نشان میدهند، مهم است. جاذب یک نقطه پایدار است که به آن «چاه» گفته میشود. دافع به عنوان یک نقطه ناپایدار در نظر گرفته میشود، که به عنوان «چشمه» نیز شناخته میشود.
نمودار نگاره فاز یک سامانه پویا مسیرهای سامانه (با فلش) و حالتهای ثابت پایدار (با نقطه) و حالتهای ثابت ناپایدار (با دایره) را در یک فضای حالت به تصویر میکشد. محورها متغیرهای حالت هستند.
مثالها
ویرایش- آونگ ساده، به تصویر (سمت راست) مراجعه کنید.
- نوسانگر هارمونیکی ساده که در آن نگاره فاز از بیضیهایی تشکیل شدهاست که در مبدأ قرار دارند، که یک نقطه ثابت است.
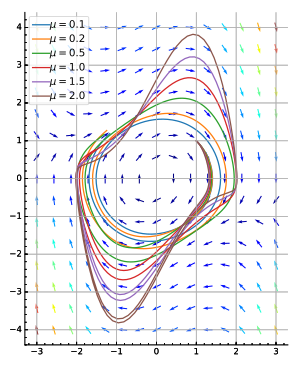
- نوسانساز ون در پل تصویر (پایین سمت راست) را ببینید.
- صفحه پارامتر (صفحه c) و مجموعه ماندبلرو
نگارههای فاز برای تجسم رفتار دستگاه معادلات دیفرانسیل معمولی
ویرایشنگاره فاز نشان دهنده رفتار جهتدار سیستم ODE است. نگاره فاز میتواند پایداری سیستم را نشان دهد.[۱]
| ناپایدار | بیشتر جوابهای سیستم به مرور زمان به سمت تمایل دارند |
| پایداری مجانبی | همه جوابهای سیستم با گذشت زمان به ۰ میرسند |
| پایداری خنثی | هیچیک از جوابهای سیستم با گذشت زمان به سمت تمایل ندارند، اما اکثر راه جوابها نیز به سمت ۰ گرایش ندارند |
رفتار نگاره فاز یک سیستم از ODEها را میتوان با مقادیر ویژه یا رَد و دترمینان (رَد ، دترمینان ) سیستم تعیین کرد.[۱]
| مقدار ویژه، رَد، دترمینان | شکل نگاره فاز |
|---|---|
| λ1 و λ2 حقیقی و دارای علامت مخالف هستند.
دترمینان < ۰ |
زینی (ناپایدار) |
| λ1 و λ2 حقیقی و هم علامت هستند، و λ1 ≠ λ2؛
۰ < دترمینان < (رَد به توان دو تقسیم بر چهار) |
گره (پایدار اگر رَد < ۰، ناپایدار در صورت رَد > ۰) |
| λ1 و λ2 هر دو مولفه حقیقی و موهومی دارند.
(رَد به توان دو تقسیم بر چهار) < دترمینان |
مارپیچ (پایدار در صورت رَد < ۰، ناپایدار در صورت رَد > ۰) |
جستارهای وابسته
ویرایشمنابع
ویرایش- ↑ ۱٫۰ ۱٫۱ ۱٫۲ ۱٫۳ Haynes Miller, and Arthur Mattuck. 18.03 Differential Equations. Spring 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA. (Supplementary Notes 26 by Haynes Miller: https://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_26.pdf)
- Jordan, D. W.; Smith, P. (2007). Nonlinear Ordinary Differential Equations (fourth ed.). Oxford University Press. ISBN 978-0-19-920824-1. Chapter 1.
- Steven Strogatz (2001). Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering. ISBN 978-0-7382-0453-6.
پیوند به بیرون
ویرایش- نگارههای فاز خطی، یک Mathlet MIT.
