عدد ثابت رامانوجان–سولدنر
(تغییرمسیر از عدد ثابت رامانوجان - سولدنر)
در ریاضیات عدد ثابت رامانوجان (همچنین به نام عدد ثابت سولدنر) یک ثابت ریاضی است که تنها صفر منحصر به فرد تابع انتگرال لگاریتم است. این ثابت پس از کاشفان آن سرینیسوا رامانوجان و یوهان سولدنر نام گذاری شدهاست.
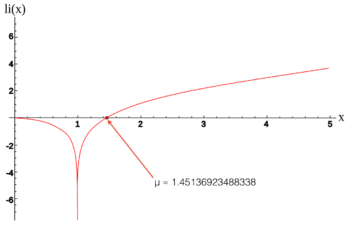
مقدار آن حدوداً برابر است با:
μ ≈ ۱٫۴۵۱۳۶۹۲۳۴۸۸۳۳۸۱۰۵۰۲۸۳۹۶۸۴۸۵۸۹۲۰۲۷۴۴۹۴۹۳۰۳۲۲۸… (دنباله A070769 در OEIS)
چون انتگرال لگاریتمی به صورت زیر تعریف شدهاست:
پس روابط زیر را داریم:
که باعث کاهش محاسبات برای اعداد صحیح مثبت میشود. همچنین چون تابع انتگرال نمایی در معادله زیر صدق میکند
بنابراین تنها صفر مثبت انتگرال نمایی در لگاریتم طبیعی ثابت رامانوجان-سولدنر رخ میدهد که مقدار آن حدوداً برابر است با:
ln(μ) ≈ ۰٫۳۷۲۵۰۷۴۱۰۷۸۱۳۶۶۶۳۴۴۶۱۹۹۱۸۶۶… (دنباله A091723 در OEIS)




