چندجملهای تیلور مقدار تقریبی یک تابع مشتقپذیر را در همسایگی یک نقطه به دست میآورد. ضرایب این چندجملهای را مشتقهای این تابع در نقطه مذکور تشکیل میدهند. این نظریه به نام ریاضیدان بروک تیلور نامیده شدهاست.
قضیه تیلور نخستین بار توسط تیلور در سال ۱۷۱۲ مطرح گردید. با این حال، بیان صریح و روشن از خطا بسیار بعدها توسط ژوزف لویی لاگرانژ ارائه شد. بیان جدید این نظریه در سال ۱۶۷۱ توسط جیمز گرگوری اشاره شده است.
قضیه تیلور در دوره سطح مقدماتی حساب دیفرانسیل و انتگرال آموزش داده شده است و از آن است که یکی از ابزار ابتدایی و اصلی در آنالیز ریاضی است. تعمیم قضیه تیلور در هندسه دیفرانسیل و معادلات دیفرانسیل با مشتقات جزئی استفاده میشود.
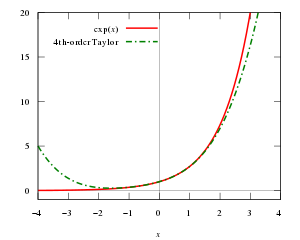
تابع توانی
y
=
e
x
{\displaystyle y=e^{x}}
اگر تابع f در نقطه a مشتق پذیر باشد و آنگاه f دارای یک تقریب خطی درنقطه a است. این به این معنی است که h1 وجود دارد:
f
(
x
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
+
h
1
(
x
)
(
x
−
a
)
,
lim
x
→
a
h
1
(
x
)
=
0.
{\displaystyle f(x)=f(a)+f'(a)(x-a)+h_{1}(x)(x-a),\qquad \lim _{x\to a}h_{1}(x)=0.}
که:
P
1
(
x
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
{\displaystyle P_{1}(x)=f(a)+f'(a)(x-a)\ }
میزان تقریب خطا:
R
1
(
x
)
=
f
(
x
)
−
P
1
(
x
)
=
h
1
(
x
)
(
x
−
a
)
.
{\displaystyle R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(x-a).\ }
که اگر بخواهیم هرچه بیشتر به نقطه a نزدیک شویم از چندجملهای درجه دوم:
P
2
(
x
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
+
f
″
(
a
)
2
(
x
−
a
)
2
.
{\displaystyle P_{2}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}.\,}
که میزان تقریب خطا:
R
2
(
x
)
=
f
(
x
)
−
P
2
(
x
)
=
h
2
(
x
)
(
x
−
a
)
2
{\displaystyle R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(x-a)^{2}\ }
به همین ترتیب اگر از چندجملهایهای درجه بالاتر استفاده کنیم بیشتر به نقطه a نزدیک میشویم.
ویرایش
تابع زیر یک تابع از درجه k از چندجملهای تیلور در نقطه a است:
P
k
(
x
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
⋯
+
f
(
k
)
(
a
)
k
!
(
x
−
a
)
k
{\displaystyle P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}}
در این صورت fوجود دارد:
f
(
x
)
=
p
(
x
)
+
h
k
(
x
)
(
x
−
a
)
k
,
lim
x
→
a
h
k
(
x
)
=
0
,
{\displaystyle f(x)=p(x)+h_{k}(x)(x-a)^{k},\quad \lim _{x\to a}h_{k}(x)=0,}
در این صورت برخورد مجانبی تابع خطا در نقطه a:
R
k
(
x
)
=
f
(
x
)
−
P
k
(
x
)
,
{\displaystyle \ R_{k}(x)=f(x)-P_{k}(x),}
برای عددی در این فاصله باز است.
ویرایش
اگر (G(t d یک تابع پیوسته در یک فاصله بسته باشد و همواره مشتق پذیر در یک فاصله باز بین a و x باشد:
R
k
(
x
)
=
f
(
k
+
1
)
(
ξ
L
)
(
k
+
1
)
!
(
x
−
a
)
k
+
1
{\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}}
بسیاری اوقات تخمین تابع خطا مفیدتر از ایجاد یک فرم کلی برای آن است. فرض کنید f یک تابع k+1 بار در بازه I شامل نقطه a مشتق پذیر است. حال فرض کنید مقادیر حقیقی q و Q وجود داشته باشند که:
q
≤
f
(
k
+
1
)
(
x
)
≤
Q
{\displaystyle q\leq f^{(k+1)}(x)\leq Q}
آنگاه تابع خطا در نامساوی:
q
(
x
−
a
)
k
+
1
(
k
+
1
)
!
≤
R
k
(
x
)
≤
Q
(
x
−
a
)
k
+
1
(
k
+
1
)
!
,
{\displaystyle q{\frac {(x-a)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(x-a)^{k+1}}{(k+1)!}},}
ویرایش
اگر f یک تابع با دامنه U از فضای حقیقی n بعدی به R باشد و همچنین f در نقطه دلخواه x عضو U مشتق پذیر باشد، میتوان نوشت:
f
(
x
+
h
)
=
f
(
x
)
+
∑
i
=
1
n
d
f
(
x
)
d
x
i
(
h
i
)
+
R
1
(
h
,
x
)
{\displaystyle f(x+h)=f(x)+\sum _{i=1}^{n}{\frac {df(x)}{dx_{i}}}(h_{i})+R_{1}(h,x)}
اگر f یک تابع با دامنه U از فضای حقیقی n بعدی به R باشد و همچنین f در نقطه دلخواه x عضو U دارای مشتقات پیوسته تا مرتبه سوم باشد، میتوان نوشت:
f
(
x
+
h
)
=
f
(
x
)
+
∑
i
=
1
n
d
f
(
x
+
t
h
)
d
x
i
(
h
i
)
+
1
/
2
∑
i
=
1
n
∑
j
=
1
n
d
f
2
(
x
+
t
h
)
d
x
i
d
x
j
+
R
2
(
h
,
x
)
.
{\displaystyle f(x+h)=f(x)+\sum _{i=1}^{n}{\frac {df(x+th)}{dx_{i}}}(h_{i})+1/2\sum _{i=1}^{n}\sum _{j=1}^{n}{\frac {df^{2}(x+th)}{dx_{i}dx_{j}}}+R_{2}(h,x).}
Apostol, Tom (1967), Calculus (به انگلیسی), Jon Wiley & Sons, Inc. {{citation }}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link )
E.Marsden,Jerrold) (2003), (به انگلیسی), Tromba,Anthony, amazon نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link ) ویکیپدیا انگلیسی