توزیع هندسی [ ۱] انگلیسی : Geometric distribution گسسته که بیانگر احتمال اولین پیروزی پس از k-1 شکست در فرایند برنولی میباشد
هندسی
تابع جرم احتمال
تابع توزیع تجمعی
پارامترها
0
<
p
≤
1
{\displaystyle 0<p\leq 1}
حقیقی )
0
<
p
≤
1
{\displaystyle 0<p\leq 1}
real ) تکیهگاه
k
∈
{
1
,
2
,
3
,
…
}
{\displaystyle k\in \{1,2,3,\dots \}\!}
k
∈
{
0
,
1
,
2
,
3
,
…
}
{\displaystyle k\in \{0,1,2,3,\dots \}\!}
تابع جرم احتمال
(
1
−
p
)
k
−
1
p
{\displaystyle (1-p)^{k-1}\,p\!}
(
1
−
p
)
k
p
{\displaystyle (1-p)^{k}\,p\!}
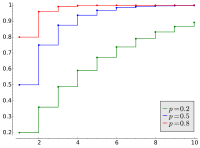
تابع توزیع تجمعی
1
−
(
1
−
p
)
k
{\displaystyle 1-(1-p)^{k}\!}
1
−
(
1
−
p
)
k
+
1
{\displaystyle 1-(1-p)^{k+1}\!}
میانگین
1
p
{\displaystyle {\frac {1}{p}}\!}
1
−
p
p
{\displaystyle {\frac {1-p}{p}}\!}
میانه
⌈
−
log
(
2
)
log
(
1
−
p
)
⌉
{\displaystyle \left\lceil {\frac {-\log(2)}{\log(1-p)}}\right\rceil \!}
−
log
(
2
)
/
log
(
1
−
p
)
{\displaystyle -\log(2)/\log(1-p)}
مُد
1
0 واریانس
1
−
p
p
2
{\displaystyle {\frac {1-p}{p^{2}}}\!}
1
−
p
p
2
{\displaystyle {\frac {1-p}{p^{2}}}\!}
چولگی
2
−
p
1
−
p
{\displaystyle {\frac {2-p}{\sqrt {1-p}}}\!}
2
−
p
1
−
p
{\displaystyle {\frac {2-p}{\sqrt {1-p}}}\!}
کشیدگی
6
+
p
2
1
−
p
{\displaystyle 6+{\frac {p^{2}}{1-p}}\!}
6
+
p
2
1
−
p
{\displaystyle 6+{\frac {p^{2}}{1-p}}\!}
آنتروپی
−
1
−
p
p
ln
(
1
−
p
)
−
ln
p
{\displaystyle -{\frac {1-p}{p}}\ln(1-p)-\ln p\!}
تابع مولد گشتاور
p
e
t
1
−
(
1
−
p
)
e
t
{\displaystyle {\frac {pe^{t}}{1-(1-p)e^{t}}}\!}
p
1
−
(
1
−
p
)
e
t
{\displaystyle {\frac {p}{1-(1-p)e^{t}}}\!}
تابع مشخصه
p
e
i
t
1
−
(
1
−
p
)
e
i
t
{\displaystyle {\frac {pe^{it}}{1-(1-p)\,e^{it}}}\!}
p
1
−
(
1
−
p
)
e
i
t
{\displaystyle {\frac {p}{1-(1-p)\,e^{it}}}\!}
P
X
(
k
)
=
P
{
X
=
k
}
=
(
1
−
p
)
k
−
1
p
{\displaystyle P_{X}(k)={\text{P}}\{X=k\}=(1-p)^{k-1}\,p}
که در آن p احتمال پیروزی در یک دفعه است.
فرض کنید آزمایشهای مستقلی با احتمال موفقیت p، آن قدر تکرار میشود تا یک موفقیت به دست آید. اگر X تعداد آزمایشهای لازم باشد، آنگاه:
P
{
X
=
n
}
=
(
1
−
p
)
n
−
1
p
n
=
1
,
2
,
3
…
{\displaystyle P\{X=n\}=(1-p)^{n-1}p\qquad n=1,2,3\ldots }
می دانیم شرط لازم و کافی برای X=n آن است که ابتدا، n-1 آزمایش شکست و n اُمین آزمایش موفقیت باشد. از آنجا که برآمدهای متوالی آزمایشها بنا به فرض مستقل هستند داریم [ ۲]
p
X
(
k
)
=
P
{
X
=
n
}
=
p
(
1
−
p
)
n
−
1
{\displaystyle p_{X}(k)={\text{P}}\{X=n\}=p(1-p)^{n-1}}
هر متغیر تصادفی که تابع جرم احتمال به صورت بالا باشد را یک متغیر (فرایند) تصادفی هندسی با پارامتر p می نامیم.
∑
n
=
1
∞
Pr
{
X
=
n
}
=
p
∑
n
=
1
∞
(
1
−
p
)
n
−
1
=
p
1
−
(
1
−
p
)
=
1
{\displaystyle \sum _{n=1}^{\infty }{\text{Pr}}\{X=n\}=p\sum _{n=1}^{\infty }(1-p)^{n-1}={\frac {p}{1-(1-p)}}=1}
در نتیجه با احتمال ۱، یک موفقیت بالاخره اتفاق می افتد. هر متغیر تصادفی که تابع جرم احتمال به صورت بالا باشد را یک متغیر تصادفی هندسی با پارامتر p مینامیم.
فرض کنیم می خواهیم رمز عبور 8 کاراکتری یک کامپیوتر را حدس بزنیم. چند مرتبه باید این کار را تکرار کنیم؟
فرض کنیم یک دارو به احتمال p سبب درمان شود، دارو روی چندمین بیمار مؤثر واقع میشود؟
فرض کنیم احتمال برد یک تیم p باشد، چند مرتبه این تیم باید بازی کند تا یک بازی را ببرد ؟
ویرایش
قصیه: امید ریاضی متغیر تصادفی هندسی با پارامتر p برابر است با
E
[
X
]
=
1
p
{\displaystyle {\text{E}}[X]={\frac {1}{p}}}
می دانیم
p
X
(
k
)
=
(
1
−
p
)
k
−
1
p
{\displaystyle p_{X}(k)=(1-p)^{k-1}p}
E
[
X
]
=
∑
x
x
p
X
(
x
)
{\displaystyle {\text{E}}[X]=\sum _{x}xp_{X}(x)}
پس با ترکیب دو رابطه ی بالا برای متغیر تصادفی هندسی داریم
E
[
X
]
=
∑
k
=
0
∞
k
(
1
−
p
)
k
−
1
p
{\displaystyle {\text{E}}[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}
حال اگر فرض کنیم
F
(
p
)
=
∑
k
=
0
∞
(
1
−
p
)
k
=
1
1
−
(
1
−
p
)
=
1
p
{\displaystyle F(p)=\sum _{k=0}^{\infty }(1-p)^{k}={\frac {1}{1-(1-p)}}={\frac {1}{p}}}
داریم
d
F
(
p
)
d
p
=
−
∑
k
=
0
∞
k
(
1
−
p
)
k
−
1
=
−
1
p
2
{\displaystyle {\frac {dF(p)}{dp}}=-\sum _{k=0}^{\infty }k(1-p)^{k-1}=-{\frac {1}{p^{2}}}}
در نتیجه
E
[
X
]
=
p
1
p
2
=
1
p
{\displaystyle {\text{E}}[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}
ویرایش
قضیه: واریانس متغیر تصادفی هندسی با پارامتر p برابر است با
var
[
X
]
=
1
−
p
p
2
{\displaystyle {\text{var}}[X]={\frac {1-p}{p^{2}}}}
فرض می کنیم پیشامد
A
=
{
X
=
1
}
{\displaystyle A=\{X=1\}}
B
=
{
X
>
1
}
{\displaystyle B=\{X>1\}}
فضای نمونه ی ما هستند، داریم
E
[
X
2
]
=
E
[
X
2
|
A
]
P
(
A
)
+
E
[
X
2
|
B
]
P
(
B
)
{\displaystyle {\text{E}}[X^{2}]={\text{E}}[X^{2}|A]{\text{P}}(A)+{\text{E}}[X^{2}|B]{\text{P}}(B)}
میدانیم
E
[
X
2
|
A
]
=
E
[
X
2
|
X
=
1
]
=
1
{\displaystyle {\text{E}}[X^{2}|A]={\text{E}}[X^{2}|X=1]=1}
و
E
[
X
2
|
B
]
=
E
[
X
2
|
X
>
1
]
=
E
[
(
X
+
1
)
2
]
=
E
[
X
2
+
2
X
+
1
]
=
E
[
X
2
]
+
2
p
+
1
{\displaystyle {\text{E}}[X^{2}|B]={\text{E}}[X^{2}|X>1]={\text{E}}[(X+1)^{2}]={\text{E}}[X^{2}+2X+1]={\text{E}}[X^{2}]+{\frac {2}{p}}+1}
بنابراین
E
[
X
2
]
=
1
×
p
+
(
E
[
X
2
]
+
2
p
+
1
)
(
1
−
p
)
{\displaystyle {\text{E}}[X^{2}]=1\times p+\left({\text{E}}[X^{2}]+{\frac {2}{p}}+1\right)(1-p)}
E
[
X
2
]
=
2
−
p
p
2
{\displaystyle {\text{E}}[X^{2}]={\frac {2-p}{p^{2}}}}
در نهایت از آنجا که
var
[
X
]
=
E
[
X
2
]
−
(
E
[
X
]
)
2
{\displaystyle {\text{var}}[X]={\text{E}}[X^{2}]-({\text{E}}[X])^{2}}
var
[
X
]
=
2
−
p
p
2
−
1
p
2
=
1
−
p
p
2
{\displaystyle {\text{var}}[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}
ویرایش
فرض کنیم می دانیم تعداد دفعاتی که سکهای را اندخته ایم از n بیشتر است، احتمال اینکه سکه را بیش از n+m دفعه بی اندازیم تا شیر بیاید چقدر است ؟
P
(
X
>
n
+
m
|
X
>
n
)
=
P
(
(
X
>
n
+
m
)
∩
(
X
>
n
)
)
P
(
X
>
n
)
=
P
(
X
>
n
+
m
)
P
(
X
>
n
)
=
(
1
−
p
)
n
+
m
(
1
−
p
)
n
=
(
1
−
p
)
m
{\displaystyle P(X>n+m|X>n)={\frac {P((X>n+m)\cap (X>n))}{P(X>n)}}={\frac {P(X>n+m)}{P(X>n)}}={\frac {(1-p)^{n+m}}{(1-p)^{n}}}=(1-p)^{m}}
پس تنها m بار پرتاب بعدی اهمیت دارد و n بار پرتاب اولیه بیارزش میشود.
همچنین میتوان ثابت کرد اگر یک متغیر تصادفی گسسته بی حافظه باشد، هندسی است. (عکس قضیه)
ویرایش
امید ریاضی متغیر تصادفی هندسی با پارامتر p برابر است با:
E
[
X
]
=
1
p
{\displaystyle E[X]={\frac {1}{p}}}
میدانیم:
P
X
(
k
)
=
(
1
−
p
)
k
−
1
p
{\displaystyle P_{X}(k)=(1-p)^{k-1}p}
و:
E
[
X
]
=
∑
x
x
P
X
(
x
)
{\displaystyle E[X]=\sum _{x}xP_{X}(x)}
پس با ترکیب دو رابطهٔ بالا برای متغیر تصادفی هندسی داریم:
E
[
X
]
=
∑
k
=
0
∞
k
(
1
−
p
)
k
−
1
p
{\displaystyle E[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}
حال اگر فرض کنیم:
F
(
p
)
=
∑
k
=
0
∞
(
1
−
p
)
k
−
1
=
1
1
−
(
1
−
p
)
=
1
p
{\displaystyle F(p)=\sum _{k=0}^{\infty }(1-p)^{k-1}={\frac {1}{1-(1-p)}}={\frac {1}{p}}}
داریم:
d
F
(
p
)
d
p
=
−
∑
k
=
0
∞
k
(
1
−
p
)
k
−
1
=
−
1
p
2
{\displaystyle {\frac {dF(p)}{dp}}=-\sum _{k=0}^{\infty }k(1-p)^{k-1}=-{\frac {1}{p^{2}}}}
در نتیجه:
E
[
X
]
=
p
1
p
2
=
1
p
{\displaystyle E[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}
ویرایش
واریانس متغیر تصادفی هندسی با پارامتر p برابر است با:
V
a
r
[
X
]
=
1
−
p
p
2
{\displaystyle Var[X]={\frac {1-p}{p^{2}}}}
فرض میکنیم پیشامد
A
=
{
X
=
1
}
{\displaystyle A=\{X=1\}}
B
=
{
X
>
1
}
{\displaystyle B=\{X>1\}}
با توجه به اینکه A و B افرازهای فضای نمونه ی ما هستند، داریم:
E
[
X
]
=
E
[
X
|
A
]
P
(
A
)
+
E
[
X
|
B
]
P
(
B
)
{\displaystyle E[X]=E[X|A]P(A)+E[X|B]P(B)}
E
[
X
2
]
=
E
[
X
2
|
A
]
P
(
A
)
+
E
[
X
2
|
B
]
P
(
B
)
{\displaystyle E[X^{2}]=E[X^{2}|A]P(A)+E[X^{2}|B]P(B)}
در نتیجه:
E
[
X
2
|
A
]
=
E
[
X
2
|
X
=
1
]
=
1
{\displaystyle E[X^{2}|A]=E[X^{2}|X=1]=1}
و:
E
[
X
2
|
B
]
=
E
[
X
2
|
X
>
1
]
=
E
[
(
X
+
1
)
2
]
=
E
[
X
2
+
2
X
+
1
]
=
E
[
X
2
]
+
2
p
+
1
{\displaystyle E[X^{2}|B]=E[X^{2}|X>1]=E[(X+1)^{2}]=E[X^{2}+2X+1]=E[X^{2}]+{\frac {2}{p}}+1}
پس:
E
[
X
2
]
=
1
∗
p
+
(
E
[
X
2
+
2
p
+
1
)
(
1
−
p
)
{\displaystyle E[X^{2}]=1*p+(E[X^{2}+{\frac {2}{p}}+1)(1-p)}
E
[
X
2
]
=
2
−
p
p
2
{\displaystyle E[X^{2}]={\frac {2-p}{p^{2}}}}
در نهایت از آنجا که میدانیم
V
a
r
[
X
]
=
E
[
X
2
]
−
(
E
[
X
]
)
2
{\displaystyle Var[X]=E[X^{2}]-(E[X])^{2}}
V
a
r
[
X
]
=
2
−
p
p
2
−
1
p
2
=
1
−
p
p
2
{\displaystyle Var[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}
![{\displaystyle {\text{E}}[X]={\frac {1}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60bd4098e8ef5223fb2d942b82cf3ab40f77e789)
![{\displaystyle {\text{E}}[X]=\sum _{x}xp_{X}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2277411c73f4c3c6f7954ded42a4a5fd4caf49e2)
![{\displaystyle {\text{E}}[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df898dc77a805a0e8561167205e0585a41005482)
![{\displaystyle {\text{E}}[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e7a4fd86d35ec4ca97168717bdaf5a2bf04024e)
![{\displaystyle {\text{var}}[X]={\frac {1-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a02418af59b01cdd292aa4c72dfa74858c805f3d)
![{\displaystyle {\text{E}}[X^{2}]={\text{E}}[X^{2}|A]{\text{P}}(A)+{\text{E}}[X^{2}|B]{\text{P}}(B)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2182d545b4726fec545ae5e8496fa7e3f780dae)
![{\displaystyle {\text{E}}[X^{2}|A]={\text{E}}[X^{2}|X=1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29c98c6c5d1242adeb1f65f1a128783325327553)
![{\displaystyle {\text{E}}[X^{2}|B]={\text{E}}[X^{2}|X>1]={\text{E}}[(X+1)^{2}]={\text{E}}[X^{2}+2X+1]={\text{E}}[X^{2}]+{\frac {2}{p}}+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1446443c0a790e8fea0162fb32a0fff8d259798e)
![{\displaystyle {\text{E}}[X^{2}]=1\times p+\left({\text{E}}[X^{2}]+{\frac {2}{p}}+1\right)(1-p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0c1e03d119da524722403f1546e1a4ecb2bc4d1)
![{\displaystyle {\text{E}}[X^{2}]={\frac {2-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c5c6ef9239a0496ba03f7519ad98ce9ea084e1)
![{\displaystyle {\text{var}}[X]={\text{E}}[X^{2}]-({\text{E}}[X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcd8feb2fcfca959ad180fc47fd9bf58bf43c152)
![{\displaystyle {\text{var}}[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48cf531ba57710c4a10cc400f065a0a558637a40)
![{\displaystyle E[X]={\frac {1}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db85df0d1c494b9c8488276e542ac7a055a92492)
![{\displaystyle E[X]=\sum _{x}xP_{X}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/828de13726190f2c8f540b9be03a0efe3d528b4c)
![{\displaystyle E[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df15d452c7936fb26678798d4df809031f85ffea)
![{\displaystyle E[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b72f1c5f97a42562501f503e015fe2d8df52f79e)
![{\displaystyle Var[X]={\frac {1-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c41f38ead7fca4aa7bc913bb5d176f3530af3e4c)
![{\displaystyle E[X]=E[X|A]P(A)+E[X|B]P(B)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b63f3757f3d61d9a0a14b5478aced73df866318c)
![{\displaystyle E[X^{2}]=E[X^{2}|A]P(A)+E[X^{2}|B]P(B)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e165ebe7afc31d44da3071e7933d5a66164b33a3)
![{\displaystyle E[X^{2}|A]=E[X^{2}|X=1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e1d1c087b6f8b22adc3bc2ff3312b91133bb08c)
![{\displaystyle E[X^{2}|B]=E[X^{2}|X>1]=E[(X+1)^{2}]=E[X^{2}+2X+1]=E[X^{2}]+{\frac {2}{p}}+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0b2dae3ffb72299b6318cda34938bec9c7af368)
![{\displaystyle E[X^{2}]=1*p+(E[X^{2}+{\frac {2}{p}}+1)(1-p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfb44ea7e9d1d5a731c3280b85298b9a500fef86)
![{\displaystyle E[X^{2}]={\frac {2-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b09c06e00b6bb269bd77967cde52e52241ddcc)
![{\displaystyle Var[X]=E[X^{2}]-(E[X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0193bfcd15632cfdb0cc694324e77bb35d356a79)
![{\displaystyle Var[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/359b44e6f580bd3b89f99282d9dac91bf8fdc849)