رمز سزار
در رمزنگاری، رمز سزار (به انگلیسی: Caesar cipher) که با نامهای کد سزار[الف]، جابهجایی سزار[ب] یا رمز جابهجایی[پ] نیز شناخته میشود، از سادهترین و شناختهشدهترین تکنیکهای رمزگذاری است.
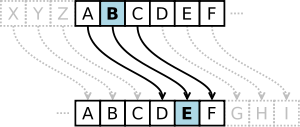
این رمز یک نوع رمز جانشینی است که در آن هر حرف در متن آشکار با حرف دیگری با فاصلهای ثابت در الفبا جایگزین میشود؛ به این فاصلهٔ ثابت «مقدار انتقال» گفته میشود.
برای مثال اگر مقدار انتقال برابر ۳ انتخاب شود و رمزنگاری روی متن با الفبای انگلیسی انجام شود، حرف D به جای حرف A مینشیند، حرف E به جای حرف B مینشیند، تا آخر. نام رمز سزار از ژولیوس سزار گرفته شدهاست که از آن در ارتباطات محرمانهٔ خود استفاده میکرد.
رمزهای جانشینی پیش از ژولیوس سزار هم استفاده میشدند. به عنوان مثال میتوان به رمز اتبش و مربع پولیبیوس اشاره کرد. اما استفاده از انتقال دورانی، نخست به نام ژولیوس سزار ثبت شدهاست. از رمز سزار حتی تا سال ۱۹۱۵ در ارتباطات نظامی استفاده شدهاست. ارتش روسیه از آن به عنوان جایگزینی برای سیستمهای پیچیدهتر که یادگیری آنها برای لشگریان دشوار بود، استفاده میکرد. در نتیجه، تحلیلگران رمز آلمانی و اتریشی پیامهای روسی را به راحتی شنود میکردند.
رمز سزار مانند تمام رمزهای جانشینی تکالفبایی دیگر به راحتی شکسته میشود و در حضور تکنیکهای مدرن رمزگشایی، هیچگونه امنیتی برای ارتباطات فراهم نمیکند. به همین دلیل، این رمز معمولاً به عنوان یکی از اجزای سیستمهای رمزگذاری پیچیدهتر مانند رمز ویژنر استفاده میشود. یک کاربرد مدرن رایج رمز سزار، روت۱۳ است که در تالارهای گفتگوی اینترنتی مورد استفاده قرار میگیرد. روت۱۳ حالت خاصی از رمز سزار است که از میزان انتقال ۱۳ استفاده میکند.
تعریف
ویرایشرمز سزار، یک رمز جانشینی تکالفبایی است، به این معنی که در این روش هر حرف از الفبای متن اصلی (الفبای آشکار) با یک حرف از الفبای رمز جایگزین میشود و این جانشینی در تمام متن به صورت یکسان صورت میگیرد. فاصلهٔ رتبهٔ هر حرف از الفبای آشکار و حرف متناظر در الفبای رمز، مقداری است ثابت که به آن «مقدار انتقال» گفته میشود. رابطهٔ بین الفبای آشکار و الفبای رمز را میتوان با همردیف کردن دو الفبا نمایش داد. الفبای رمز درواقع همان الفبای آشکار است که به میزان مشخصی به سمت راست یا چپ چرخانده شدهاست. برای مثال، رمز سزار با چرخش به چپ به میزان انتقال ۳، در جعبهٔ پایین نمایش داده شدهاست. کلید رمز همان مقدار انتقال است که در این مثال برابر با ۳ انتخاب شدهاست.[۱]
| الفبای آشکار | ABCDEFGHIJKLMNOPQRSTUVWXYZ
|
|---|---|
| الفبای رمز | DEFGHIJKLMNOPQRSTUVWXYZABC
|
همچنین بهطور مشابه میتوان جدول زیر را برای الفبای فارسی درنظر گرفت:
| الفبای آشکار | ا ب پ ت ث ج چ ح خ د ذ ر ز ژ س ش ص ض ط ظ ع غ ف ق ک گ ل م ن و ه ی
|
|---|---|
| الفبای رمز | ت ث ج چ ح خ د ذ ر ز ژ س ش ص ض ط ظ ع غ ف ق ک گ ل م ن و ه ی ا ب پ
|
تبدیل حروف آشکار به رمز در تمام متن یکسان است و به این ترتیب رمز سزار در ردهٔ رمزهای تکالفبایی (در برابر رمزهای چند الفبایی) قرار میگیرد.[۲]
رمزگشایی به روش مشابه و با انتقال به همان میزان در جهت عکس انجام میشود.
مثال
ویرایشبرای رمزگذاری متن، کافی است که هر حرف از متن آشکار با حرف متناظر آن در الفبای رمز جایگزین شود. در مثال زیر از کلید ۳ برای رمزگذاری استفاده شدهاست.
| متن آشکار | THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
|
|---|---|
| متن رمز | WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
|
به طور مشابه میتوان از رمز سزار با کلید ۳ برای رمزگذاری متن فارسی استفاده کرد:
| متن آشکار | ژولیوس سزار نظامی اهل روم بود
|
|---|---|
| متن رمز | صاوپاض ضشتس یفتهپ تبو ساه ثاز
|
تعریف ریاضی
ویرایشرمز سزار را میتوان به صورت ریاضی با استفاده از همنهشتی نمایش داد. به این منظور ابتدا با استفاده از الگوی سادهٔ زیر، حروف الفبا با اعداد جایگزین میشوند.[۳]
سپس هر حرف x با انتقال n به ترتیب زیر رمزگذاری میشود:[۴]
به طریق مشابه، رمزگشایی به صورت زیر انجام میشود:
توجه به این نکته ضروری است که تعاریف مختلفی برای عملیات پیمانه (mod) وجود دارد. در اینجا نتیجهٔ پیمانه عددی بین ۰ تا ۲۵ است. یعنی اگر x+n یا x-n در بازهٔ ۰ تا ۲۵ نباشد، باید ۲۶ با نتیجه جمع یا از آن کم شود.[۵]
وجه تسمیه
ویرایشنام رمز سزار از ژولیوس سزار گرفته شدهاست. ژولیوس سزار، نظامی و سیاستمدار اهل جمهوری روم در قرن اول پیش از میلاد بود که نقش مهمی در گسترش قلمرو روم و تبدیل آن از جمهوری به امپراتوری داشت. به گفته سوئتونیوس، ژولیوس سزار از انتقالی به میزان ۳ (D به جای A در رمزگذاری[ت]) برای رمز کردن پیامهای مهم نظامی استفاده میکرد.[۷] رمزهای جانشینی پیش از ژولیوس سزار هم استفاده میشدند. به عنوان مثال میتوان به رمز اتبش و مربع پولیبیوس اشاره کرد. اما استفاده از انتقال دورانی، نخست به نام ژولیوس سزار ثبت شدهاست. شواهدی وجود دارد که ژولیوس سزار از سیستمهای پیچیدهتری نیز استفاده کردهاست، اما اطلاعی از جزئیات آن در دسترس نیست.[۸][۹] برای مثال، سیستم جابجایی ستونی نیز در برخی منابع به ژولیوس سزار نسبت داده میشود و با نامهایی همچون جعبه سزار[ث] یا مربع سزار[ج] خوانده میشود.[۱۰]
تاریخچهٔ استفاده
ویرایشدورهٔ باستان
ویرایشبعد از ژولیوس سزار، نوهٔ خواهر او آگوستوس نیز از رمز سزار استفاده میکرد، با این تفاوت که از انتقالی به میزان ۱ استفاده میکرد و الفبا را به صورت دورانی در نظر نمیگرفت. به این ترتیب، او از B به جای A و در انتهای الفبا به جای Z از AA استفاده میکرد.[۱۱][۱۲]
دقیقاً مشخص نیست که رمز سزار در زمان خود تا چه حد مؤثر بودهاست، اما احتمالاً امنیت قابل قبولی داشتهاست. نباید فراموش کرد که بخش زیادی از دشمنان سزار بیسواد بودند و گروهی دیگر نیز فرض میکردند پیام به یک زبان خارجی ناشناخته نوشته شدهاست.[۱۳] تکنیک ثبتشدهای برای شکستن رمزهای جانشینی ساده از آن دوران وجود ندارد. اولین اثر ثبتشده در این مورد به تحقیقات ابویوسف کندی در زمینهٔ تحلیل فراوانی در قرن نهم میلادی بر میگردد.[۱۴]
کاربرد رمز سزار در دوران باستان به زبان لاتین محدود نبود. در پشت طومارهای مزوزا، عبارت "כוזו במוכסז כוזו" به الفبای عبری نوشته میشد. این عبارت شامل سه نام خدا در زبان عبری است که با استفاده از رمز سزار با کلید ۱، رمزگذاری شدهاند. قدمت مزوزا، به زمان حضور بنیاسرائیل در صحرای سینا نسبت داده میشود.[۱۵] اما استفاده از رمز سزار در پشت آن، رسمی است که احتمالاً از زمان سلطهٔ روم بر یهودیه، که یهودیان اجازهٔ استفاده از مزوزا را نداشتند، باقی ماندهاست. این حروف رمز خود یک نام الهی بااهمیت تلقی میشوند که طبق اعتقادات یهودیان ارتدکس قدرتهای شیطانی را مهار میکند.[۱۶]
قرون جدید
ویرایشدر قرن نوزدهم میلادی، گاهی از قسمت آگهیهای شخصی روزنامهها برای انتقال پیامهای رمز شده استفاده میشد. برای مثال، نمونههایی از استفاده از این رمز در روزنامهٔ تایمز دیده میشود.[۱۷] از رمز سزار حتی تا سال ۱۹۱۵ در ارتباطات نظامی استفاده شدهاست. ارتش روسیه از آن به عنوان جایگزینی برای سیستمهای پیچیدهتر که یادگیری آنها برای لشگریان دشوار بود، استفاده میکرد. در نتیجه، تحلیلگران رمز آلمانی و اتریشی پیامهای روسی را به راحتی شنود میکردند.[۱۸][۱۹]
در رمز ویژنر از الگوریتم رمز سزار استفاده میشود، با این تفاوت که کلیدهای رمز (میزان انتقال) متفاوتی برای حروف متن آشکار در نظر گرفته میشود. به این ترتیب کلید رمز کلی یک عدد چند رقمی (یک کلمه) است. اگر طول کلمهٔ کلید با طول متن آشکار یکسان باشد، به صورت تصادفی تولید شده باشد و تنها یک بار استفاده شود، پد یکبار مصرف حاصل میشود که غیرقابل شکست است.[۲۰] دشواری در دستیابی به این شرایط و نیز مشکل توزیع امن چنین کلید رمزی مابین طرفین ارتباط، در عمل باعث میشود که پد یکبار مصرف مورد استفاده قرار نگیرد. کلیدهای کوتاهتر از متن آشکار باعث ایجاد الگوهای تکرارشونده در متن رمز میشوند که با روشهای آماری پیشرفته در تحلیل فراوانی امکان شکست رمز را فراهم میکند. نیروهای ایالات مؤتلفهٔ آمریکا در طول جنگ داخلی آمریکا از رمز ویژنر با کلیدهای Manchester Bluff، Complete Victory و Come Retribution استفاده میکردند که برای طرف مقابل شناختهشده بود.[۲۱]
استفادههای اخیر
ویرایشرمز سزار امروزه در بعضی اسباببازیهای کودکان استفاده میشود. همچنین در الگوریتم روت۱۳ از رمز سزار استفاده میشود. روت۱۳ حالت خاصی از رمز سزار با کلید رمز ۱۳ بر روی الفبای انگلیسی است. با توجه به آنکه الفبای انگلیسی از ۲۶ حرف تشکیل شدهاست، روت ۱۳ وارون خودش است. به این معنی که عملیات رمزگذاری و رمزگشایی عیناً مانند یکدیگر هستند. روت۱۳ در یوزنت بهطور گسترده برای پنهان کردن متن (برای مثال، پاسخ معماها و افشاسازها) استفاده میشود اما کاربردی برای امنیت ارتباط ندارد.[۲۲]
در آوریل ۲۰۰۶، برناردو پروونتسانو پدرخواندهٔ فراری مافیا به دلیل بیدقتی و استفاده از رمز سزار در پیامهای مخفی، شناسایی و دستگیر شد. پروونتسانو در این سیستم از کلید ۳ و برای نوشتن پیام از اعداد به جای حروف استفاده میکرد. به این ترتیب، ۲۱ حرف الفبای ایتالیایی از A تا Z به ترتیب با اعداد ۴ تا ۲۴ جایگزین میشدند. به عنوان مثال، به جای A عدد ۴ نوشته میشد، به جای B عدد ۵ و الی آخر.[۲۳][۲۴]
در سال ۲۰۱۱ رجب کریم که از رمز سزار برای تماس با یک فعال اسلامگرای اهل بنگلادش و برنامهریزی برای بمبگذاری در هواپیماهای بریتیش ایرویز استفاده کرده بود، محاکمه و به زندان محکوم شد. کریم و همدستش با وجود آشنایی با سیستمهای پیشرفتهتر از قبیل پیجیپی و تروکریپت، از یک نسخهٔ رمز سزار که خودشان در نرمافزار اکسل نوشته بودند استفاده میکردند، چون به باور آنان سیستمهای پیشرفته برای «کفار» شناختهشده بودند.[۲۵]
شکستن رمز
ویرایش| میزان انتقال رمزگشایی |
متن آشکار احتمالی |
|---|---|
| ۰ | EXXEGOEXSRGI |
| ۱ | DWWDFNDWRQFH |
| ۲ | CVVCEMCVQPEG |
| ۳ | BUUBDLBUPODF |
| ۴ | ATTACKATONCE |
| ۵ | ZSSZBJZSNMBD |
| ۶ | YRRYAIYRMLAC |
| ... | |
| ۲۳ | HAAHJRHAVUJL |
| ۲۴ | GZZGIQGZUTIK |
| ۲۵ | FYYFHPFYTSHJ |
رمز سزار حتی در شرایط حملهٔ متن اصلی به راحتی قابل شکسته شدن است. دو موقعیت زیر میتوانند در نظر گرفته شوند:
- حملهکننده میداند یا حدس میزند که نوعی از رمز جانشینی ساده استفاده شدهاست اما مشخصاً نمیداند که رمز سزار است.
- حملهکننده میداند که رمز سزار استفاده شدهاست اما مقدار انتقال را نمیداند.
در حالت اول، استفاده از تکنیکهای معمول شکستن رمزهای جانشینی، مانند تحلیل فراوانی، به سادگی نتیجهبخش است. در حین استفاده از این تکنیکها، حملهکننده به راحتی متوجه نظم موجود در سیستم جانشینی و استفاده از رمز سزار خواهد شد.[۲۶]
شکستن رمز در حالت دوم سادهتر از حالت اول است. از آنجا که تعداد ممکن انتقالها محدود است (در زبان انگلیسی ۲۶ حالت ممکن) اعمال حملهٔ جستجوی فراگیر و آزمایش تمام حالات ممکن به سرعت انجام میشود.[۲۷] برای مثال، همانطور که در جدول نشان داده شدهاست، بخشی از متن به همراه تمام انتقالهای ممکن نوشته میشود و ردیف حاوی متن بامعنی به راحتی قابل تشخیص است. در این روش کافی است که زیر هر حرف از متن رمز شده، تمام حروف الفبا به ترتیب نوشته شود.[۲۸][۲۹] در مثال جدول روبرو، متن رمز شده EXXEGOEXSRGI است و به سادگی میتوان تشخیص داد که کلید رمز استفاده شده برابر با ۴ بودهاست.
روش دیگر، حملهٔ جستجوی فراگیر با کمک تحلیل فراوانی است. در این روش، با مقایسهٔ فراوانی حروف در متن رمز و فراوانی حروف در متون عادی زبان مورد استفاده و جابجایی دو نمودار، میتوان میزان انتقال را پیدا کرد. برای مثال، در زبان انگلیسی E و T پراستفادهترین و حروف Q و Z کماستفادهترین حروف هستند.[۳۰][۳۱] این روش توسط کامپیوتر هم قابل پیادهسازی است. برای این کار کافی است با استفاده از آزمون مربع کای، توزیع داده شده با توزیع مورد انتظار مقایسه شود.[۳۲]
معمولاً فقط یک متن آشکار محتمل برای یک متن رمز وجود دارد، اما برای رمزهای بسیار کوتاه ممکن است تعداد پاسخهای محتمل بیشتر از یکی باشد. برای مثال، متن رمز MPQY میتواند به ADEN یا KNOW برگردد. بهطور مشابه ALIIP میتواند DOLLS یا WHEEL باشد و AFCCP را میتوان به JOLLY یا CHEER رمزگشایی کرد. به حداقل طول متن رمز شده که لازم است تا متن اصلی به صورت یکتا قابل شناسایی باشد، فاصلهٔ یکتایی گفته میشود.[۳۳]
استفادهٔ چندباره از رمز سزار بر روی یک متن، به امنیت بیشتر منجر نمیشود. زیرا دو بار رمزگذاری با انتقالهای A و B معادل یک بار رمزگذاری با کلید A+B است. به زبان ریاضی میتوان گفت مجموعهٔ رمز سزار با کلیدهای متنوع، تحت ترکیب یک گروه تشکیل میدهند.[۳۴]
یادداشتها
ویرایشپانویس
ویرایش- ↑ Beutelspacher, Cryptology, 5.
- ↑ Wobst, Cryptology unlocked, 35.
- ↑ Luciano and Prichett، «Cryptology: From Caesar Ciphers to Public-Key Cryptosystems»، The College Mathematics Journal، 3.
- ↑ Wobst, Cryptology unlocked, 19.
- ↑ Wobst, Cryptology unlocked, 19.
- ↑ "Latin alphabet". Encyclopædia Britannica (به انگلیسی). Retrieved 25 May 2022.
- ↑ Suetonius, “LVI”, The Lives of the Twelve Caesars, Volume 01: Julius Caesar.
- ↑ Reinke، «Classical Cryptography»، The Classical Journal، 114.
- ↑ Singh, The Code Book, 26-27.
- ↑ Sutherland, Cracking Codes & Cryptograms for Dummies, 34-35.
- ↑ Suetonius, “LXXXVIII”, The Lives of the Twelve Caesars, Volume 02: Augustus.
- ↑ Bauer, Decrypted Secrets: Methods and Maxims of Cryptology, 47.
- ↑ Pieprzyk, Fundamentals of computer security, 6.
- ↑ Singh, The Code Book, 34-35.
- ↑ Poltorak, Alexander. "Mezuzah History and Customs" (به انگلیسی). chabad.org. Retrieved 27 May 2022.
- ↑ Poltorak, Alexander. "Mezuzah and Astrology" (به انگلیسی). chabad.org. Archived from the original on 18 September 2020. Retrieved 12 June 2020.
- ↑ Kahn, The Codebreakers – The Story of Secret Writing, 775-776.
- ↑ Wobst, Cryptology unlocked, 20.
- ↑ Bauer, Decrypted Secrets: Methods and Maxims of Cryptology, 47.
- ↑ Luciano and Prichett، «Cryptology: From Caesar Ciphers to Public-Key Cryptosystems»، The College Mathematics Journal، 7.
- ↑ Kahn, The Codebreakers – The Story of Secret Writing, 217-221.
- ↑ Wobst, Cryptology unlocked, 20.
- ↑ Leyden, John (19 April 2006). "Mafia boss undone by clumsy crypto" (به انگلیسی). The Register. Archived from the original on 12 June 2020. Retrieved 12 June 2020.
- ↑ Lorenzi, Rossella (17 April 2006). "Mafia Boss's Encrypted Messages Deciphered" (به انگلیسی). Discovery news. Archived from the original on 8 October 2006. Retrieved 14 June 2022.
- ↑ "BA jihadist relied on Jesus-era encryption" (به انگلیسی). The Register. 22 March 2011. Archived from the original on 12 June 2020. Retrieved 12 June 2020.
- ↑ Beutelspacher, Cryptology, 9-11.
- ↑ Beutelspacher, Cryptology, 8-9.
- ↑ Leighton، «Secret Communication among the Greeks and Romans»، Technology and Culture، 153.
- ↑ Sinkov, Elementary cryptanalysis: A Mathematical Approach, 13-15.
- ↑ Singh, The Code Book, 37.
- ↑ Luciano and Prichett، «Cryptology: From Caesar Ciphers to Public-Key Cryptosystems»، The College Mathematics Journal، 5.
- ↑ Savarese, Chris; Hart, Brian (26 April 2010). "The Caesar Cipher" (به انگلیسی). Archived from the original on 24 May 2020. Retrieved 15 June 2020.
- ↑ Menezas, Handbook of Applied Cryptography, 246.
- ↑ Wobst, Cryptology unlocked, 31.
منابع
ویرایش- Bauer, Friedrich (1997). Decrypted Secrets: Methods and Maxims of Cryptology (به انگلیسی). Springer.
- Beutelspacher, Albrecht (1994). Cryptology (به انگلیسی). Mathematical Association of America.
- Kahn, David (1967). The Codebreakers – The Story of Secret Writing (به انگلیسی). Macmillan.
- Leighton, Albert C. (April 1969). "Secret Communication among the Greeks and Romans". Technology and Culture (به انگلیسی). 10 (2): 139–154. Retrieved 8 June 2020 – via JSTOR.
- Luciano, Dennis; Prichett, Gordon (January 1987). "Cryptology: From Caesar Ciphers to Public-Key Cryptosystems". The College Mathematics Journal (به انگلیسی). 18 (1): 2–17. Retrieved 9 June 2020 – via JSTOR.
- Menezas, Alfred (1996). "Chapter 7 - Block Ciphers" (PDF). Handbook of Applied Cryptography (به انگلیسی). CRC Press. Retrieved 23 November 2020.
- Pieprzyk, Josef (2003). Fundamentals of computer security (به انگلیسی). Springer.
- Reinke, Edgar C. (December 1962). "Classical Cryptography". The Classical Journal (به انگلیسی). 58 (3): 113–121. Retrieved 8 June 2020 – via JSTOR.
- Singh, Simon (1999). The Code Book (به انگلیسی). Fourth State.
- Sinkov, Abraham (1968). Elementary cryptanalysis: A Mathematical Approach (به انگلیسی). New York: Random House.
- Suetonius (121). The Lives of the Twelve Caesars, Volume 01: Julius Caesar (به انگلیسی).
- Suetonius (121). The Lives of the Twelve Caesars, Volume 02: Augustus (به انگلیسی).
- Sutherland, Denise; Koltko-Rivera, Mark E. (2010). Cracking Codes & Cryptograms for Dummies (به انگلیسی). Wiley.
- Wobst, Reinhard (2007). Cryptology unlocked (به انگلیسی). Wiley.