مکانیک کلاسیک
مکانیک کلاسیک علمیست که در آن حرکت اشیاء ماکروسکوپیک باسرعتی غیرنسبیتی (خیلی کمترازسرعت نور) از پرتابه گرفته تا بخشهایی از ماشینآلات و اشیاء نجومی مانند فضاپیماها، سیارهها، ستارهها و کهکشان را توصیف میکند.

اگر وضعیت کنونی یک شیء شناخته شود، میتوان با قوانین مکانیک کلاسیک پیشبینی کرد که چگونه در آینده حرکت خواهد کرد؛ (جبرگرایی)، و چگونه در گذشته حرکت کردهاست (برگشتپذیری).
نخستین پیشرفت مکانیک کلاسیک اغلب به عنوان مکانیک نیوتنی یاد میشود. این شامل مفاهیم فیزیکی به کار رفته و روشهای ریاضیاتی است که توسط آیزاک نیوتن ، گوتفرید ویلهلم لیبنیتز و دیگران در سدهٔ ۱۷ میلادی اختراع شدهاست تا حرکت اجسام فیزیکی را تحت تأثیر سیستمی از نیروها توصیف کند.
بعداً، روشهای انتزاعیتری ایجاد شد که منجر به تغییر ساختار مکانیک کلاسیک موسوم به مکانیک لاگرانژی و مکانیک همیلتونی گردید. این پیشرفتها، که عمدتاً در سدههای ۱۸ و ۱۹ صورت گرفته، بهویژه از طریق استفادهٔ آنها از مکانیک تحلیلی، فراتر از کارهای نیوتن است. آنها با برخی اصلاحات در همهٔ زمینههای فیزیک نوین نیز مورد استفاده قرار میگیرند.
مکانیک کلاسیک نتایج بسیار دقیقی را در هنگام مطالعهٔ اشیاء بزرگ که خیلی گسترده نیستند و سرعت آنها به سرعت نور نزدیک نیست، فراهم میکند. زمانیکه اشیاء مورد بررسی اندازهٔ یک قطر اتم را دارند، لازم است که رشتهٔ فرعی اصلی دیگر مکانیک: مکانیک کوانتومی نیز معرفی شود. برای توصیف سرعتهایی که در مقایسه با سرعت نور کوچک نیستند، نسبیت خاص ضروری است. در صورتی که اشیاء خیلی بزرگ شوند، نسبیت عام قابل اجرا میشود. با این حال، تعدادی از منابع نوین شامل مکانیک نسبیت به فیزیک کلاسیک، که از نظر آنها مکانیک کلاسیک را در پیشرفتهترین و دقیقترین شکل خود نشان میدهد، میباشند.[note ۱]
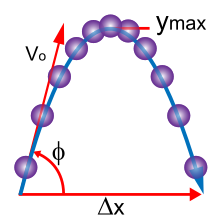
در زیر مفاهیم اساسی مکانیک کلاسیک معرفی شدهاست. برای سادگی، اغلب اشیاء دنیای واقعی را به عنوان ذرات نقطهای (اشیاء با اندازهٔ ناچیز) مدلسازی میکنند. حرکت یک ذرهٔ نقطهای با تعداد کمی از پارامترها مشخص میشود: موقعیت، جرم و نیروهای اعمال شده بر روی آن، هر یک از این پارامترها به نوبهٔ خود بحث شدهاست.
در واقعیت، نوع اشیایی که مکانیک کلاسیک میتواند توصیف کند، همیشه اندازهٔ غیر صفر دارد. (فیزیک ذرات بسیار ریز مانند الکترون توسط مکانیک کوانتومی با دقت بیشتری توصیف میشود) اشیاء با اندازهٔ غیر صفر رفتار پیچیدهتری نسبت به ذرات اشیای نقطهای فرضی دارند؛ زیرا درجههای آزادی اضافی، به عنوان مثال، یک توپ بیسبال میتواند در حین حرکت بچرخد. با این حال، نتایج ذرات نقطهای میتواند برای مطالعهٔ چنین اشیایی با استفاده از آنها بهعنوان اشیاء کامپوزیت، که از تعداد زیادی ذرات نقطهای جمعی ساخته شدهاست، مورد استفاده قرار گیرد. مرکز جرم یک مادهٔ کامپوزیت مانند یک ذرهٔ نقطهای رفتار میکند.
مکانیک کلاسیک از مفاهیم عقل سلیم دربارهٔ چگونگی وجود ماده و نیروها و تعامل استفاده میکند. فرض بر این است که ماده و انرژی دارای ویژگیهای مشخص و معقولی مانند مکان در فضا و سرعت هستند. مکانیک غیر نسبیتی نیز فرض میکند که نیروها فوراً عمل میکنند. (همچنین به عمل از راه دور مراجعه کنید)
موقعیت و مشتقات آن
ویرایش| موقعیت | م |
| موقعیت زاویهای / زاویه | بیواحد (رادیان) |
| سرعت | m · s −1 |
| سرعت زاویهای | s −1 |
| شتاب | m · s −2 |
| شتاب زاویهای | s −2 |
| پرتاب | متر · −3 |
| «پرتاب زاویهای» | −3 |
| انرژی خاص | m 2 · s −2 |
| میزان دوز جذب شده | m 2 · s −3 |
| ممان اینرسی | کیلوگرم · متر 2 |
| تکانه | kg · m · s s1 |
| حرکت زاویهای | kg · m 2 · s s 1 |
| نیرو | kg · m · s −2 |
| گشتاور | kg · m 2 · s s2 |
| انرژی | kg · m 2 · s s2 |
| توان | kg · m 2 · s s3 |
| فشار و چگالی انرژی | kg · m · 1 · s s2 |
| کشش سطحی | کیلوگرم s 2 |
| ثابت فنر | کیلوگرم s 2 |
| تابش و جریان انرژی | کیلوگرم s 3 |
| اصطحکاک جنبشی | m 2 · s −1 |
| گرانروی | kg · m − 1 · s −1 |
| چگالی (تراکم جرم) | کیلوگرم · متر 3 |
| چگالی (تراکم وزن) | kg · m · 2 · s s2 |
| چگالی عددی | متر 3 |
| عمل | kg · m 2 · s s 1 |
موقعیت یک ذرهٔ نقطهایای در رابطه با یک دستگاه مختصات با محوریت یک نقطهٔ مرجع ثابت دلخواه در فضا به نام مبدأ O تعریف میشود. یک دستگاه مختصات ساده ممکن است موقعیت یک ذره P را با یک بردار اقلیدسی نشان داده شده توسط یک فلش برچسب r که از مبدأ O تا نقطهٔ P امتداد مییابد را، توصیف کند. بهطور کلی، ذرهٔ نقطهای نیازی نیست که نسبت به O ثابت باشد. در مواردی که P در حال حرکت نسبت به O است، r بهعنوان یک تابعی از t، زمان تعریف میشود. در نسبیت پیش از انیشتین (معروف به نسبیت گالیله)، زمان به عنوان مطلق در نظر گرفته میشود، یعنی فاصلهٔ زمانی که میان هر جفت معین از وقایع مشاهده شود برای همهٔ ناظران یکسان است.[۱] مکانیک کلاسیک علاوهبر اتکا به زمان مطلق و هندسهٔ اقلیدسی را برای ساختار فضا فرض میکند.[۲]
سرعت
ویرایشسرعت یا سرعت تغییر موقعیت با زمان به عنوان مشتقی از موقعیت با توجه به زمان تعریف میشود:
- .
در مکانیک کلاسیک، سرعت بهطور مستقیم افزوده و کاسته میشود. به عنوان مثال، اگر یک اتومبیل با سرعت ۶۰ کیلومتر بر ساعت به سمت شرق در حرکت باشد و از اتومبیل دیگری که در همان مسیر با سرعت ۵۰ کیلومتر در ساعت حرکت میکند عبور میدهد، اتومبیل کندتر درک میکند که سرعت حرکت اتومبیل سریعتر برابر با 60 − ۵۰ = 10 km/h میباشد. با این حال، از منظر اتومبیل سریعتر، اتومبیل آهستهتر به میزان ۱۰ کیلومتر بر ساعت کندتر حرکت میکند، که اغلب به عنوان -۱۰ نشان داده در جهت عکس نشان داده میشود. سرعتها به عنوان مقادیر برداری بهطور مستقیم افزایشی هستند. آنها باید با استفاده از تجزیه و تحلیل برداری مورد بررسی قرار گیرند.
نیوتن اصول فلسفهٔ طبیعی خود را در سه قانون پیشنهادی حرکت ایجاد کرد: قانون اینرسی، قانون دوم شتاب او (که در بالا ذکر شد)، و قانون عمل و عکس العمل؛ و از این رو پایه و اساس مکانیک کلاسیک را بنا نهاد. هر دو قانون دوم و سوم نیوتن در علوم علمی و ریاضیات مناسب در کتاب اصول ریاضی فلسفهٔ طبیعی نیوتن مورد استفاده قرار گرفت . در اینجا آنها از تلاشهای پیشین برای توضیح پدیدههای مشابه، که یا ناقص، نادرست یا بیان ریاضی کمی دقیقتری داشتند، متمایز میشوند. نیوتن همچنین اصول حفظ ممان و ممان زاویهای را به کار برد. در مکانیک، نیوتن نیز نخستین کسی بود که نخستین فرمول صحیح علمی و ریاضی گرانش را در قانون گرانش جهانی نیوتن ارائه داد. ترکیبی از قوانین حرکت و گرانش نیوتن کاملترین و دقیقترین توصیف مکانیک کلاسیک را ارائه میدهد. وی نشان داد که این قوانین در مورد اشیاء روزمره و نیز اشیای آسمانی اعمال میشود. بهطور ویژه، او توضیح نظری خود را در مورد قوانین حرکت کپلر سیاهها ارائه داد.
یادداشتها
ویرایش- ↑ The notion of "classical" may be somewhat confusing, since this term usually refers to the era of classical antiquity in European history. While many discoveries within the mathematics of that period are applicable today and of great use, much of the science that emerged from that time has since been superseded by more accurate models. This in no way detracts from the science of that time as most of modern physics is built directly upon those developments. The emergence of classical mechanics was a decisive stage in the development of science, in the modern sense of the term. Above all, it is characterized by an insistence that more rigor be used to describe the behavior of bodies. Such an exacting foundation is only available through mathematical treatment and reliance on experiment, rather than speculation. Classical mechanics established a way to predict the behavior of objects in a quantitative manner and ways to test these predictions through carefully designed measurement. The emerging globally cooperative endeavor provided increased scrutiny and testing of both theory and experiment. This remains a key factor in establishing certainty in knowledge and in bringing it to the service of society. History shows how closely the health and wealth of a society depend on nurturing this investigative and critical approach.
منابع
ویرایش- ↑ Knudsen, Jens M.; Hjorth, Poul (2012). Elements of Newtonian Mechanics (illustrated ed.). Springer Science & Business Media. p. 30. ISBN 978-3-642-97599-8.
- ↑ MIT physics 8.01 lecture notes (page 12) بایگانیشده در ۲۰۱۳-۰۷-۰۹ توسط کتابخانه کنگره بایگانیهای اینترنت (PDF)