درگاه:ریاضیات/مفاهیم
مفاهیم ۱
e یک عدد حقیقی منحصر بفرد است، به طوری که مقدار مشتق تابع در نقطهٔ x = 0 برابر ۱ شود. از این طریق تابع به عنوان تابع نمایی و تابع معکوس آن، به عنوان تابع لگاریتم طبیعی یا لگاریتم در مبنای e معرفی میشود. از طرفی میتوان e را به عنوان مبنای تابع لگاریتم طبیعی (با استفاده از انتگرال)، به عنوان حد یک دنباله ریاضی یا به عنوان حد یک سری ریاضی تعریف کرد. گاهی عدد e، به افتخار ریاضیدان سوئیسی، لئونارد اویلر، عدد اویلر نامیده میشود.
مفاهیم ۲

نسبت طلایی در ریاضیات و هنر هنگامی است که «نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر» باشد. تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید».تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.
مفاهیم ۳

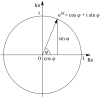
قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانون کسینوسها هنگامی که زاویهٔ بین دو بردار ۹۰ درجهاست میباشد. این قضیه به نام ریاضیدان یونانی فیثاغورس نامگذاری شدهاست. به سخن دیگر در یک مثلث راستگوشه (قائم الزاویه) همواره مجموع توانهای دوم دو ضلع برابر با توان دوم ضلع سوم است.
قانون کسیونسها بیان میکند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند.
بردار مجموع از رابطهٔ بدست میآید.
مفاهیم ۴
تابع یکی از مفاهیم نظریه مجموعهها و حساب دیفرانسیل و انتگرال است. بطور ساده میتوان گفت که به قاعدههای تناظری که به هر ورودی خود یک و فقط یک خروجی نسبت میدهند، تابع گفته میشود. تابع به عنوان مفهومی در ریاضیات، توسط گوتفرید لایبنیتس در سال ۱۶۹۴، با هدف توصیف یک کمیت در رابطه با یک منحنی مانند شیب یک نمودار در یک نقطه خاص به وجود آمد. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم.
مفاهیم ۵

انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل میدهند. اولین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است. از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شدهاست. هر گاه معادله مشتق تابعی معلوم باشد وبخواهیم معادله اصلی تابع را تعیین کنیم این عمل را تابع اولیه مینامیم.
مفاهیم ۶

بینهایت مفهومی است که در رشتههای مختلف ریاضیات (با تعبیرات مختلف)معمولاً به معنای «فراتر از هر مقدار» است. معمولاً نشانه بینهایت در ریاضیات است. بی نهایت از واژه لاتین finites به معنی محدود گرفته شده ( علامت ) چیزی است که "محدود" نیست، که در آن هیچ محدودیت فضایی و زمانی وجود ندارد. در آنالیز حقیقی، بینهایت به معنای حدی بیکران است. یعنی متغیر فراتر از هر مقدار در نظرگرفته شده رشد میکند. جدا از تمام این مساعل ریاضی قانون های ساخته شده توسط انسان است ، که برای درک چیزی که بدون ان قادر به درک مساعل نبوده ، با داشتن قانون ها قادر به درک ، فهم و چگونگی ان خواهد بود .
مفاهیم ۷
مفاهیم ۸
مفاهیم ۹
مفاهیم ۱۰
مفاهیم ۱۱
مفاهیم ۱۲
مفاهیم ۱۳
مفاهیم ۱۴
مفاهیم ۱۵
مفاهیم ۱۶
مفاهیم ۱۷
مفاهیم ۱۸
مفاهیم ۱۹
مفاهیم ۲۰
مفاهیم ۲۱
مفاهیم ۲۲
مفاهیم ۲۳
مفاهیم ۲۴
مفاهیم ۲۵
مفاهیم ۲۶
مفاهیم ۲۷
مفاهیم ۲۸
مفاهیم ۲۹
مفاهیم ۳۰
مفاهیم ۳۱
مفاهیم ۳۲
مفاهیم ۳۳
مفاهیم ۳۴
مفاهیم ۳۵
مفاهیم ۳۶
مفاهیم ۳۷
مفاهیم ۳۸
مفاهیم ۳۹
مفاهیم ۴۰
مفاهیم ۴۱
مفاهیم ۴۲
مفاهیم ۴۳
مفاهیم ۴۴
مفاهیم ۴۵
مفاهیم ۴۶
مفاهیم ۴۷
مفاهیم ۴۸
مفاهیم ۴۹
مفاهیم ۵۰
مفاهیم ۵۱
مفاهیم ۵۲
مفاهیم ۵۳
مفاهیم ۵۴
مفاهیم ۵۵
مفاهیم ۵۶
مفاهیم ۵۷
مفاهیم ۵۸
مفاهیم ۵۹
مفاهیم ۶۰
مفاهیم ۶۱
مفاهیم ۶۲
مفاهیم ۶۳
مفاهیم ۶۴
مفاهیم ۶۵
مفاهیم ۶۶
مفاهیم ۶۷
مفاهیم ۶۸
مفاهیم ۶۹
مفاهیم ۷۰
مفاهیم ۷۱
مفاهیم ۷۲
مفاهیم ۷۳
مفاهیم ۷۴
مفاهیم ۷۵
مفاهیم ۷۶
مفاهیم ۷۷
مفاهیم ۷۸
مفاهیم ۷۹
مفاهیم ۸۰
مفاهیم ۸۱
مفاهیم ۸۲
مفاهیم ۸۳
مفاهیم ۸۴
مفاهیم ۸۵
مفاهیم ۸۶
مفاهیم ۸۷
مفاهیم ۸۸
مفاهیم ۸۹
مفاهیم ۹۰
مفاهیم ۹۱
مفاهیم ۹۲
مفاهیم ۹۳
مفاهیم ۹۴
مفاهیم ۹۵
مفاهیم ۹۶
مفاهیم ۹۷
مفاهیم ۹۸
مفاهیم ۹۹



![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)



