سهمی
در ریاضیات سَهمی (به انگلیسی: Parabola) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. این منحنی که شَلجَمی یا شَلغَمی[۱] هم نامیده میشود یکی از مقاطع مخروطی میباشد، زیرا از تقاطع یک صفحه و یک مخروط میتواند به وجود بیاید.[۲] سهمی و هذلولی دو مقطع مخروطی باز هستند و بیضی و دایره دو مقطع مخروطی بسته.

| از سلسله مقالاتی دربارهٔ مقاطع مخروطی | |
 | |
| سهمی | |
|---|---|
| معادله | |
| گریز از مرکز () | |
| نیمراستوتر کانونی () | |
  | |
| هذلولی | |
| معادله | |
| گریز از مرکز () | |
| نیمراستوتر کانونی () | |
  | |
| بیضی | |
| معادله | |
| گریز از مرکز () | |
| نیمراستوتر کانونی () | |
  | |
| دایره (حالت خاص بیضی) | |
| معادله | |
| گریز از مرکز () | |
| نیمراستوتر کانونی () | |
 | |
| • • • | |

تاریخچه
ویرایشیونان باستان
ویرایشبنابر تقریظی از اراتوستن، سهمی را نخستینبار منایخموس (۳۸۰ — ۳۲۰ پ. م)، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خطکش و پرگار) کشف کرد. آپولونیوس برای اولین بار نام «پارابول» (یونانی: παραβολή، به معنای «کاربرد»)[الف] را بر روی سهمی گذاشت[۳] و اقلیدس (حدود ۳۶۵–۲۷۵ پ. م) بررسی دقیقی از ویژگیهای سهمی ارائه کرد.[۴] پاپوس اسکندرانی (حدود ۳۵۰ — ۲۹۰ پ. م) مفهوم خطهای هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی نسبت ثابتی (که بعدها به برونمرکزی معروف شد) دارد و این نسبت ثابت برای همهٔ سهمیها برابر ۱ است.[۵]
نام آپولونیوس (اواخر قرن سوم — اوایل قرن دوم پیش از میلاد) برای قرنها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است،[۶] با مطالعهٔ مخروط آغاز میکند و پس از تعریف سه مقطع مخروطی (سهمی، هذلولی، و بیضی)، به تعریف خط مماس آنها میپردازد و سپس ثابت میکند که فاصلهٔ کانونی برای همهٔ نقاط روی یک بیضی ثابت است.[۷]
قرون وسطی
ویرایشهمزمان با حکومت مأمون در خراسان (در قرن سوم هجری)، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخهای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانهای را ابداع کرد که میتوان آن را مقدمهای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخهای کاملتر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهدهدار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است.[۶] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آنها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند[ب] و برای واژهٔ «پارابولی» اصطلاح «مکافی» را در نظر گرفتند که معنای آن را حفظ میکند[پ] و هنوز در زبان عربی به بیضی «قطع ناقص» گفته میشود.[۶]
رنسانس و قرون جدید
ویرایشاسحاق نیوتن در کتاب «اصول ریاضی فلسفه طبیعی»[۸] نشان داد که اگر نیروی کشش میان اجسام آسمانی متناسب با معکوس مجذور فاصله بین آن دو باشد، اجرامی که به دور یک جرم بزرگ میگرداند، یا باید حرکت دایرهای، بیضوی، سهموی یا هذلولوی داشته باشند. نیوتن از سهمی برای محاسبه مدار شهاب سنگها استفاده کرد.[۹] امروزه میدانیم که اگر چه سهمی مدل خوبی برای حرکت شهاب سنگها میباشد ولی این مدل از دقت بالایی برخوردار نیست و به ندرت مدار شهاب سنگها با دقت بسیار بالایی سهموی میباشند.[۱۰]
گالیله نشان داد که وقتی جسمی را در هوا پرتاب میکنیم، مسیر حرکت آن سهموی میباشد.[۱۱] این موضوع زمانی صحت دارد که از مقاومت هوا و آثار چرخشی چشم پوشی شود.[۲]
نیوتون و گرگوری نشان دادند که هنگامی که نور به صورت موازی به یک آینه سهموی تابانده شود، پس از انعکاس در کانون آن جمع میشود.[۱۱]
پاسکال سهمی را تصویر یک دایره در نظر گرفت.[۱۱]
رنه دکارت خود مقاطع مخروطی آپولونیوس، بهویژه بیضی و سهمی، را در آثارش در باب هندسه تحلیلی بررسی کرده بود.[۱۲]
پس از نیوتن
ویرایشکاربرد
ویرایشاقتصادیترین شکل پل کمانی در اغلب شرایط عملی سهمی میباشد.[۱۳]
تعریف سهمی
ویرایشسهمی به عنوان مقطع مخروطی
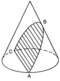
ویرایشسهمی خمی باز است که از برخورد مخروطی قائم با قاعدهٔ دایرهای و صفحهای حاصل میشود که با یکی از وترهای مخروط موازی باشد ولی با ارتفاع مخروط موازی نباشد.[۱۴] اگر این صفحه با قاعدهٔ مخروط موازی باشد حاصل دایره، اگر با ارتفاع مخروط موازی باشد حاصل هذلولی، و اگر با هیچیک از وترهای مخروط یا ارتفاع آن موازی نباشد حاصل بیضی خواهد بود.[۱۵]
تعریف سهمی به صورت مکان هندسی نقاط
ویرایشدر صفحهٔ اقلیدسی سهمی را میتوان به صورت مجموعه ای از نقاط (مکان هندسی) تعریف کرد.
سهمی مکان هندسی نقاطی است که فاصلهٔ آنها از نقطه ای ثابت به نام کانون با فاصلهٔ آن از خط ثابتی به نام خط هادی برابر باشد.
معادله
ویرایشمعادله ساده سهمی: میباشد. شکل کلی معادله سهمی در دستگاه مختصات دکارتی، به شکل زیر است:
که ضرایب تا همگی ثابت و حقیقی بوده، یا غیر صفر هستند، و همچنین .
مختصات قطبی
ویرایشاگر p > 0 سهمی ای با معادلهٔ دکارتی (سهمی به سمت راست باز میشود) دارای معادلهٔ قطبی زیر است:
- ( ).
محور سهمی و کانون آن است.
اگر مبدأ را به سمت کانون جابه جا کنیم یعنی معادله ی قطبی زیر را خواهیم داشت:
روش انتقال
ویرایش
- a بیانگر باز و بسته شدن دهانه تابع است.
- h بیانگر جابجا شدن نمودار در جهت افقی. (برخلاف علامت h حرکت میکند)
- k بیانگر جابجا شدن نمودار در جهت عمودی. (برجهت علامت k حرکت میکند)
در معادله بالا h باعث انتقال افقی و k باعث انتقال عمودی میشود. کافیست نمودار رسم کرده و با توجه به علامت h و k آن را منتقل میکنیم.
مساحت زیر سطح سهمی
ویرایشمساحت زیر سطح سهمی که منحنی و تابعی است براساس این روش بیان می گردد
مساحت زیر سطح سهمی بر اساس و رابطه مختصات دوبعدی قطبی بدست می آید. و چون در مختصات واحد مختصات سهمی2واحد بیشتر است به علاوه دو می کنیم
خاصیت بازتاب نور
ویرایشخاصیت بازتاب سهمی بیان میدارد که اگر یک سهمی آیینه ای باشد و بتواند نور را بازتاب کند، آنگاه نورهایی که موازی با خط تقارن سهمی به آن وارد میشوند، به سمت کانون آن بازتاب میکنند.
اثبات
ویرایشدر شکل مقابل F نقطه کانون سهمی، P نقطه ای دلخواه روی سهمی، PT عمودی بر خط هادی سهمی و MP نیم ساز زاویه FPT∠ است. Q نقطه ای دیگر روی سهمی است و QU نیز عمود بر خط هادی است. ما میدانیم FP = PT و FQ = QU. به وضوح، QT > QU, پس QT > FQ. اما از طرفی تمام نقاط روی MP از F و T به یک فاصله هستند. یعنی هیچ نقطه ای روی سهمی نیست که روی MP باشد؛ که یعنی خط مماس به سهمی که از نقطه T میگذرد، نیمساز FP و PT است. با توجه به این که زاویه تابش نور از خط مماس به منحنی با زاویه بازتاب برابر است، میتوان دریافت که پرتو بازتاب در راستای همان خطی است که به F میرود.
ویژگیها
ویرایش- معادلهٔ سهمی در یک سیستم مختصات تخصیصیافته عبارت است از . رأس این سهمی در قرار دارد و محور ها محور تقارن آن است.[۱۶]
- نقطه تمرکز سهمی بر روی محور تقارن قرار دارد و گسترندهٔ سهمی (منحنی مکان هندسی مرکز انحناهای آن) تنها یک نوک تیز دارد.[۱۷]
- خط تمرکز معادل است که عمود بر محور ها است و فاصلهاش از نقطهٔ تمرکز ( ) برابر است.[۱۸]
- برای هر نقطهٔ روی سهمی، فاصلهٔ از نقطهٔ تمرکز فاصلهٔ آن از خط تمرکز است.[۱۹]
- همهٔ سهمیها با هم متشابهاند.[۲۰]
- سهمیهایی با برابر با یکدیگر همنهشتند.[۲۱]
- فرمول پارامتریک سهمی: نمونهٔ آن میتواند باشد.[۲۲]
رسم سهمی
ویرایشمعادلهٔ درجه دو را در نظر میگیریم. برای رسم سهمی کافیست که رأس آن را پیدا کنیم.
فرمول رأس سهمی برابر است با:
بعد از پیدا کردن رأس سهمی دو نقطهٔ دیگری را با جایگذاری در فرمول پیدا کرده و نمودار را رسم میکنیم.
نکته: اگر در معادله درجه دو a مثبت باشد دهانه سهمی رو به بالا و اگر منفی باشد دهانه سهمی رو به پایین است.
نگارخانه
ویرایش-
یک توپ جهنده که مسیر آن با استروبسکوپ ۲۵ تصویر بر ثانیه نشان داده شدهاست.توپ پس از هر جهش به طور قابل توجهی غیر کروی میشود مخصوصا بعد از جهش اول که همراه با گردش توپ به دور خودش و مقاومت هوا، باعث میشود مسیر حرکت توپ با سهمی فرق کند.
-
مسیر حرکت سهموی آب در یک آبنما.
-
پل رینبو (به انگلیسی: Rainbow Bridge) که بر روی رودخانهٔ نیاگارا قرار دارد و کانادا (در سمت چپ) را به آمریکا (در سمت راست) متصل میکند. قوس سهموی زیر پل وزن جاده را تحمل میکند.
-
شکل سهمی وار که بر اثر چرخش به وجود آمدهاست.دو مایع با چگالیهای متفاوت فضای باریک بین دو صفحهٔ شفاف پلاستیکی را پر میکنند.فضای خالی بین صفحهها از بالا پایین و کنارهها بسته شدهاست کل مجموعه حول محوری عمودی که از مرکز میگذرد در گردش است.
-
اجاق خورشیدی ساخته شده با آینهٔ سهموی.
-
میکروفون سهمیوار با بازتاب دهندهٔ پلاستیکی شفاف، که به منظور گوش دادن به گفت و گوی داور در یک بازی فوتبال کالجی آمریکایی استفاده شدهاست.
-
نورافکن ادیسون که به ارابه ای متصل شدهاست و دارای آینه ای سهموی است.
-
استیفن هاوکینگ در یک هواگرد که بر مسیری سهموی پرواز میکند تا جاذبهٔ صفر را شبیه سازی کند.
-
مسیر دنباله دار Kohoutek (به رنگ قرمز) هنگامی که از منظومهٔ شمسی داخلی میگذرد. این مسیر شکلی نزدیک به سهمی دارد .دایرهٔ آبی مدار زمین را نشان میدهد.
-
استفاده از قوسهای سهموی در معماری
یادداشت
ویرایش- ↑ بر خلاف نامی که آپولونیوس بر بیضی (الیپسیس، به معنای کمتر بودن) و هذلولی (هایپربول، به معنای بیشتر بودن) گذاشت و به کمتر یا بیشتر بودن برونمرکزی این منحنیها از عدد ۱ اشاره دارد، دلیل انتخاب پارابول برای سهمی واضح نیست.
- ↑ شاید به این دلیل که اصطلاحات بیگانه بهسادگی در ساختار زبان عربی پذیرفته نمیشود.
- ↑ در معادلهٔ آپولونیوس برای بیضی مقدار کاسته میشود و «ناقص» در «قطع ناقص» به همین امر اشاره دارد. معادلهٔ آپولونیوس برای هذلولی مشابه معادلهٔ بیضی است با این تفاوت که مقدار به مقدار اضافه میشود، ازینرو مترجمان عربی آن، هذلولی را «قطع زائد» نامیدند. معادلهٔ آپولونیوس برای سهمی هم است و چون در آن بخش ناقص و زائدی نیست مترجمان عربی برای آن معادل «مُکافی» (به معنی همکفو و برابر) را برگزیدند.[۶]
پانویس
ویرایشآموزش رسم سهمی «سیده فاطمه موسوی نطنزی»
منابع
ویرایشپانویس
ویرایش- ↑ "معنی شلغمی | لغتنامه دهخدا" شکلی مانند شلغم، سهمی، عربی آن را شلجم خوانند. http://www.vajehyab.com/dehkhoda/%D8%B4%D9%84%D8%BA%D9%85%DB%8C
- ↑ ۲٫۰ ۲٫۱ Encyclopædia Britannica, parabola (mathematics)
- ↑ Coolidge 1945:4
- ↑ Wolfram MathWorld 2002
- ↑ Coolidge 1945:10
- ↑ ۶٫۰ ۶٫۱ ۶٫۲ ۶٫۳ هوخندایک و امینی ۱۳۹۲:۸۶–۹۸
- ↑ Coolidge 1945:14-25
- ↑ Principia
- ↑ Encyclopædia Britannica, comet (astronomy): The impact of Newton’s work
- ↑ Roger R. Bate, Donald D. Mueller, Jerry E. White, Fundamentals of astrodynamics, Dover Publications, 1971, p. 24
- ↑ ۱۱٫۰ ۱۱٫۱ ۱۱٫۲ Weisstein, Eric W. «Parabola" From MathWorld--A Wolfram Web Resource
- ↑ Mazer 2011:39
- ↑ John Thomas Rule, Steven A. Coons, "Graphics", McGraw-Hill (New York), 1961, p. 137
- ↑ Encyclopedia Britannica
- ↑ University of Denver 2002
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
- ↑ Pottmann et al. 2007:235
فهرست منابع
ویرایش- Pottmann, Helmut; Asperl, Andreas; Hofer, Michael; Kilian, Axel; Bentley, Daril (2007). Architectural geometry. Bentley Institute Press. ISBN 1-934493-04-X. OCLC 180177477.












